NetworkXを用いた社会的経済的ネットワークの分析 |
ネットワーク理論、別名で、グラフ理論は、グラフ・ネットワークに関する研究領域です。ネットワークで扱える対象は、通信ネットワーク、物流ネットワーク、鉄道ネットワーク、エネルギーネットワーク、経済社会ネットワークなどが典型です。ネットワーク理論では、工学的な領域では、最短路問題、最小費用流問題、最大マッチング問題、経済社会的な領域では、金融システムの安定化問題、イノベーションの波及問題、感染症拡大対策などが取り扱われています。簡単なグラフ(ネットワーク)理論の解説については、ネットワーク理論入門(pdfファイルです)を参照ください。
ネットワークは、頂点(vertex, node)と辺(edge, arc)からなる構造、グラフ構造を特徴としています。通常、頂点や辺は、重み(weight)などの属性を持ちます。ネットワークでは、辺の重み(weight)も考慮します。
Pythonでは、グラフ・ネットワークを扱うライブラリーとしてNetworkXがあります。 NetworkXを使うと、色々なアルゴリズムを使えます。コマンドプロンプトで、pip install -U networkx と入力すると、インストールできます
Anacondaを用いてPythonをインストールすると、networkxも一括してインストールされるので、即座に利用可能となります。Colabolatory を利用して networkx を実行することもできます。ここでは、Pythonのsite-package networkxがインストールされていることを前提とします。グラフを表示するためには、matplotlibパッケージが必要なので、この使用方法についても知識があると想定します。matplotlib の知識がない読者は、PythonのページにあるTutorial を参照して下さい。
networkx は バージョンが neworkx 2.5 にアップデートされています。コードの仕様がかなり変更されていますので、 networkx 1.x を前提に書かれたコードは重大なエラーを出します。以下のコードは networkx 2.x で書かれたものです。 networkX の公式サイトは こちらになります。以下で使用するサンプルコードは この github にあります。また、このページで使用する networkX のサンプルもこの Colaboratory にアップされていますので、自由に活用ください。
(Last updated:2021/1/16)
簡単なネットワーク作成の方法 |
networkx は以下のようにインストールできます。
$ pip install networkx $ pip install pygraphviz
PyGraphviz は Graphviz を用いてグラフを描くときに必要となります。
networkx の簡単な使用法を説明します。ネットワークを作成するためには、作成するネットワークに名前を付ける必要がある
import networkx as nx G=nx.Graph()
と記述すると、 名前がGという(空の)ネットワークが作成される。このGに必要なノード(node)とエッジ、リンク(edges)を付け加えて、作成すべきネットワークを構成して行く。以下の例は10個のノードからなるネットワークを描くscriptである。Nをノードの集合とすると
N=[1,2,3,4,5,6,7,8,9,10] G.add_nodes_from(N)
で、Nで与えられたノードをネットワーク G に加えられます。Eをエッジの集合として、
E= [(1,2),(1,8),(2,3),(2,4),(4,5),(6,7),(6,8),(8,9),(8,10)] G.add_edges_from(E)
と書くと、集合Eのエッジをもつネットワークが作成されます。ちなみに、ペア(8,10) はノード8とノード10の間にエッジが存在することを表現します。以上までのコードをまとめると、
# -*- coding: utf-8 -*- # creating a new network import networkx as nx G = nx.Graph() N=[1,2,3,4,5,6,7,8,9,10] E= [(1,2),(1,8),(2,3),(2,4),(4,5),(6,7),(6,8),(8,9),(8,10)] G.add_nodes_from(N) G.add_edges_from(E)
となっています。作成されたネットワークのグラフを描くためには、matplotlib.pyplot を用いる場合は
import matplotlib.pyplot as plt nx.draw_networkx(G,with_labels=True, node_color='r')
と記述する必要があります。グラフ G を作成して、それを図示するプログラムは以下のようになります。
# -*- coding: utf-8 -*-
# creating a new network
import networkx as nx
G = nx.Graph()
N=[1,2,3,4,5,6,7,8,9,10]
E= [(1,2),(1,8),(2,3),(2,4),(4,5),(6,7),(6,8),(8,9),(8,10)]
G.add_nodes_from(N)
G.add_edges_from(E)
# drawing the created network
import matplotlib.pyplot as plt
nx.draw_networkx(G,with_labels=True, node_color='r')
plt.axis('off')
plt.title('an example')
plt.savefig("example.png") # save as png
plt.show()
# drawing 以下の記述はこのネットワークをグラフィックに描くコードになっています。このscriptを実行すると、以下のようなネットワークの図が表示される。plt.savefig('example.png')は'example'という名前の画像ファイルをpng形式で保存させるための命令文です。
上の例では、グラフを描くのに Matplotlib を利用しました。NetworkX の主たる目的はグラフを描くパッケージではないが、 networkx.drawing モジュールを活用してグラフを描くことができます。以下のように使用できます。 このコードでは、グラフの作成に DiGraph が使用されていますが、これは有向グラフ(directed graph)を作成することを指します。エッジに方向があります。[3, 5, 4, 1, 6, 2, 7, 8, 9, 7]は、エッジの方向が、3 -> 5 -> 4 -> 1 ... -> 7 となっていることを表現します。図示されたグラフを見ればよくわかります。 PyGraphvizを使うと、Matplotlib や networkx.drawing を使うよりも、ネットワークモデルらしい形状の見た目になります。ただし、PyGraphvizをインストールする必要があります。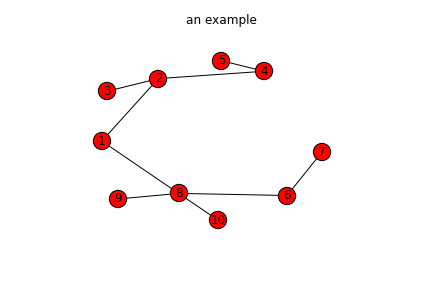
import networkx as nx
G = nx.DiGraph()
nx.add_path(G, [3, 5, 4, 1, 6, 2, 7, 8, 9, 7])
nx.add_path(G, [3, 0, 6, 4, 2, 7, 1, 9, 8, 5])
nx.draw(G, with_labels=True, font_weight='bold')
$ pip install pygraphviz
とインストールする。add_path () を使用して、ノード間のパスを設定することもできます。ノードは自動的に作成されます。add_path () を用いたコードは以下の通りです。これを実行してみて下さい。
import networkx as nx G = nx.DiGraph() nx.add_path(G, [3, 5, 4, 1, 0, 2, 7, 8, 9, 6]) nx.add_path(G, [3, 0, 6, 4, 2, 7, 1, 9, 8, 5]) nx.nx_agraph.view_pygraphviz(G, prog='fdp')
G.nodes, G.edges, G.adj and G.degree を用いて、4つの基本的なグラフの性質を表示することができます。これらはネットワークを構成する nodes, edges, neighbors (adjacencies), degrees of nodes を集合的に表現しています。 ちなみに、
list(G.nodes) list(G.edges) list(G.adj[1]) # or list(G.neighbors(1))
と利用できます。
Networkxのグラフ作成関数を用いた例 |
ここでは、ネットワークを作成する組み込み関数generatorsを用いて、グラフを表示する例を提示します。組み込み関数generatorsに関する解説はこのサイトにあります。以下で取り上げるErdos and Reneyi モデルなどに関する理論的な解説については、 network_theoryのページを参照ください。pdfファイルです。
ランダムネットワークを描いてみましょう。最もシンプルで典型的なランダム・ネットワークの理論モデルは、 Erd̈os and Renyi 型ネットワークです。基本的な考え方は、以下の通りである。n 個のノードから任意に2つのノードを選び、例えば、サイコロを振って 6 の目が出たら、このノード間にリンクを張る。それ以外の目が出たとき何もしない。再び、任意に2つのノードを選び、サイコロを振って 6 の目が出たら、このノード間にリンクを張る。それ以外の目が出たとき何もしない。これを何回も続ける。この結果、ある種のネットワークが形成される。この手続きに従って形成されるネットワークをランダムネットワークという。
最初にランダムネットワークの例として、組み込み関数 erdos_renyi_graph(n, p)を用いる。利用するコードは以下の通りです。
# Erdos Renyi graph
import matplotlib.pyplot as plt
import networkx as nx
G=nx.erdos_renyi_graph(100,0.1)
plt.figure(1)
nx.draw_random(G)
plt.savefig("Erdos_Renyi.png") # save as png
plt.show()
degree_sequence=sorted(G.degree(),reverse=True) # degree sequence
print ("Degree sequence", degree_sequence)
# the drawing of histogram of the data
import numpy as np
kukan=range(0,20)
hist, kukan=np.histogram(degree_sequence,kukan,density=True)
plt.figure(2)
plt.plot(hist)
plt.xlabel('degree')
plt.ylabel('frequency')
plt.title('degree frequency(Erdos_Renyi net : n=100, p=0.1)')
plt.grid(True)
plt.savefig("ER_degree.png") # save as png
plt.show()
このプログラムは以下のようなグラフを表示します。グラフもランダムに描かれるので、全く同じグラフは表示されません。
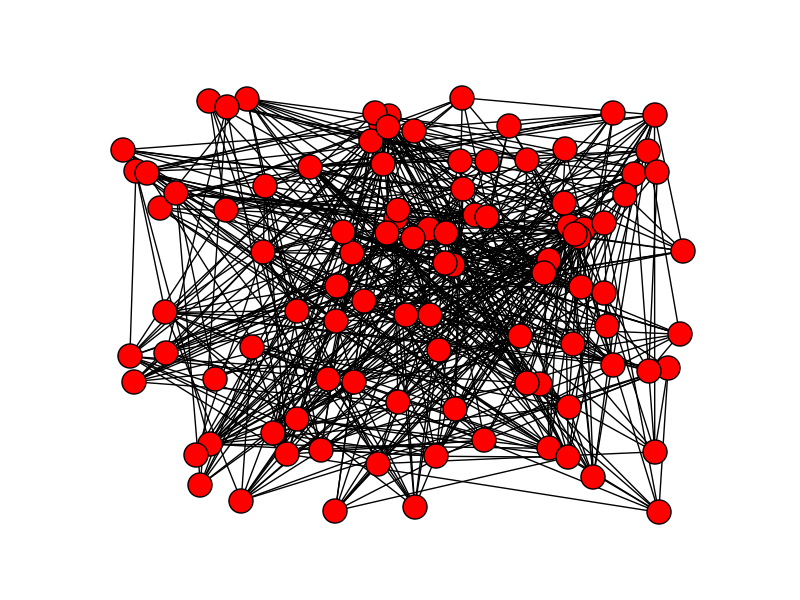
ノード総数が\(n\)、連結確率が\(p\)であるとき、エルデシュ・レーニイ型ランダム・ネットワークの次数分布は平均値\((n-1)p\)のポアッソン分布に(近似的に)従うことが知られている。このケースでは、\(n=100,p=0.1\)である。
一応、理論的解説をしておきましょう。ノードの集合\(N=\{1,2,\ldots, n\}\)の中から、任意に選び出した二つのノード間にリンクが張られる確率(リンク形成確率)を、各ノードの位置に依存せず、\(p\)とする。
各ノードはネットワーク上の\(n-1\)個のノードとリンクされる可能性があるが、\(n-1\)個のノードのうち\(d\)個のノードとリンク接続している確率は
\[ p^d (1-p)^{n-1-d} \]である。\(n-1\)個の中から\(d\)個のノードを取り出す組合せの数は
\[ \binom{n-1}{d}=\frac{(n-1)!}{d!(n-d-1)!} = \frac{n\dots (n-d-2)}{d!} \]である。従って、任意に選ばれたノードの次数が\(d\)となる確率は
\[ \Pr(d) = \binom{n-1}{d} p^d (1-p)^{n-1-d} \]である。平均次数は
\[ \sum_{d=0}^{n-1}Pr(d)d =(n-1)p \]である。形成されるネットワーク上のリンク総数は確率変数であるが、大数の法則により、\(n\)が非常に大きくなるとき、リンク総数平均値は
\[ \frac{n(n-1)}{2}p \]となることが知られている。各ノードの集中化(クラスタリング)係数が\(p\)になることは自明である。さらに、 \(n\)が非常に大きくなるときには、パラメター\(\mu =(n-1)p\)を平均値としてもつポアッソン分布になる。
\[ \Pr(d) = \frac{e^{-\mu} \mu^d}{d!} ,\; d =0,1,2,\dots n-1. \]この次数分布で表現されるネットワークをポアッソン型ランダム・ネットワーク(Poisson random graph)ともいう。Erd̈os and Renyi 型ネットワークはポアッソン分布をしたランダム・ネットワークの一つの例です。
このErd̈os and Renyi のランダムネットワークの次数分布は以下の図に示されている。正確なポアッソン分布とは異なりますが、近似的な形状をしていることが分かる。
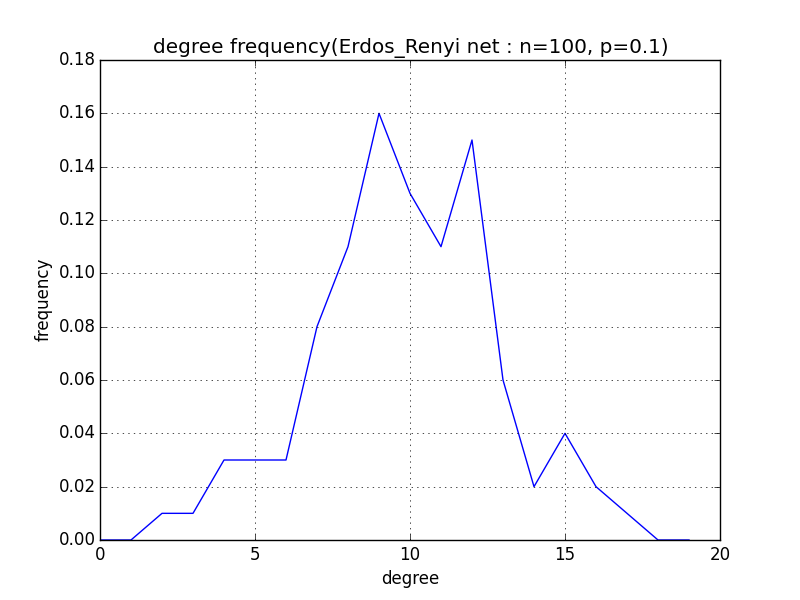
社会ネットワークの研究で最もよく知られている例はスモール・ワールド(small worlds)という言葉で表現されているモデルであろう。スモール・ワールドという言葉が意味することは、現実の社会ネットワークではネットワークの直径が想像されるよりもはるかに小さく、パスの平均距離が短いという事実である。Milgram(1967)は、現実社会におけるネットワークのパス距離がいかほどかを調べるために実験を行った。ネブラスカに住む住人96人を電話帳から任意に選び、彼らに封書を送った。封書の中には、ハーバード大学名入りの”パスポート”が封入されていて、これをMilgramの(ボストンに住む)友人(A氏とする)に送り返すような願い書が入っていた。この友人A氏に関する情報は住所と職業だけが開示されていた。封書を受け取った人々は、A氏を直接・間接に知っているであろうと予想される友人に、あるいは同じ職業に就いている友達に、”パスポート”を送ることを要請された。これを受け取った人々も同じように行動することが要請されていた。この結果、18個の”パスポート”がA氏のもとに届いた。平均的に5.9回の転送を経由して届いたことが判明した。人々は世界中の誰とでも6次の隔たり(six degrees)でつながっている。世界は見たよりもはるかに小さい事実を発見した。
一般的に、人々が平均的に100人の友人・知人を持っているとすると、友人の友人数は10000名となる。従って、友人の友人の友人の数は100万人となる。人々が平均的に\(d\)個のリンク(友人)を持っていると、距離6のパスによって到達可能なノード数は\(x=d^6\)である。両辺の対数を取ると、\(\ln x = 6 \times \ln d\)から\(x = 200,000,000\)(人口が2億人)とおくと、米国の人々の平均的友人数\(d\)は約24.1人となる。
その後、スモール・ワールド・モデルはWatts and Strogatz(1998)によってネットワークモデルとして定式化され、スモール・ワールド性がWWWネットワークにおいても観測できることがWatts(1999)によって確認されている。
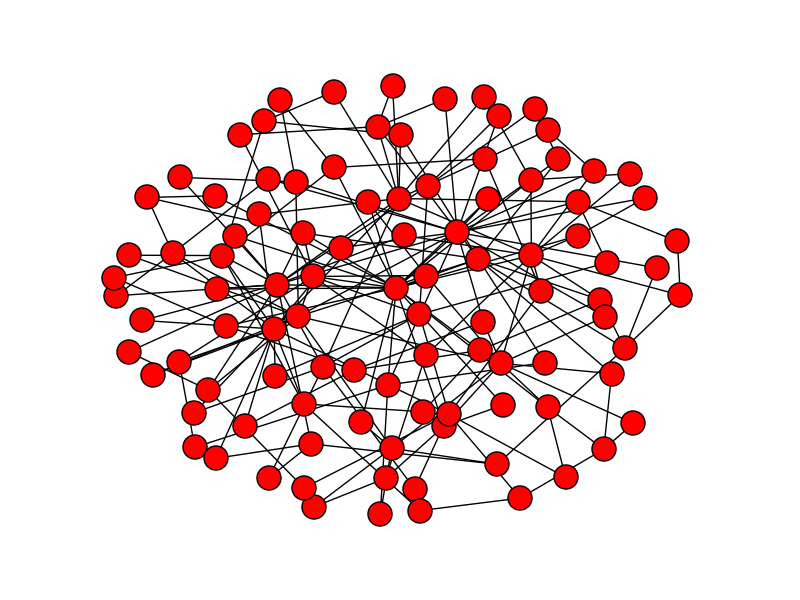
スモールワールド・ネットワークを描いてみましょう。ここでの例は、ノード総数100で、各ノードが4人の隣人に連結している初期状態から、確率0.2でこのリンクを外してランダムに選んだ他のノードに連結されるというアルゴリズムになっています。いわゆるWatts_Strogatz型のモデルである。組み込み関数はwatts_strogatz_graph(n, k, p)を用います。このコードは以下のようになります。
# Watts Strogatz graph
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
G=nx.watts_strogatz_graph(100,4,0.2)
plt.figure(1)
nx.draw(G) #nx.draw_random(G)
plt.savefig("smallworld.png") # save as png
plt.show()
degree_sequence=sorted(G.degree(),reverse=True) # degree sequence
print ("Degree sequence", degree_sequence)
kukan=range(0,20)
hist, kukan=np.histogram(degree_sequence,kukan,density=True)
# drawing the degree sequence
plt.figure(2)
plt.plot(hist)
plt.xlabel('degree')
plt.ylabel('frequency')
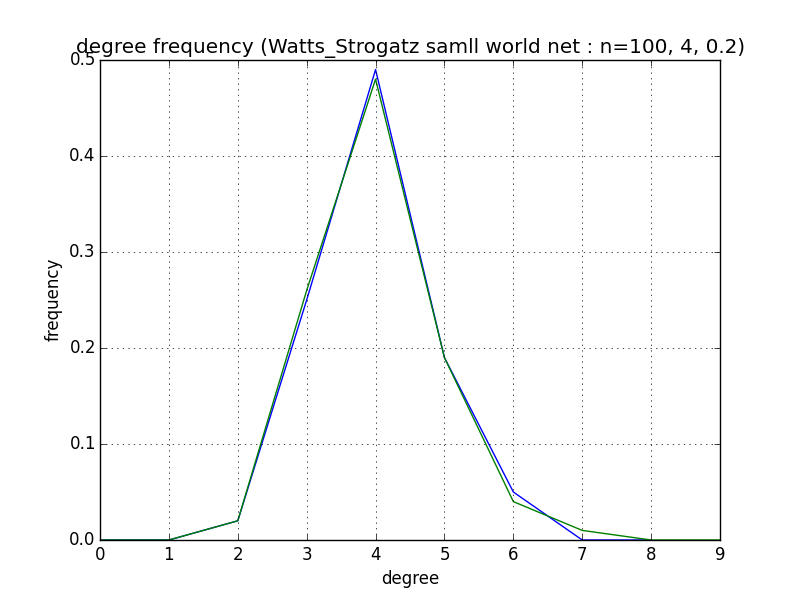
plt.title('degree frequency (Watts_Strogatz samll world net : n=100, 4, 0.2)')
plt.grid(True)
plt.savefig('SW_degree.png')
plt.show()
このコードでは、ネットワークは組み込み関数 watts_strogatz_graph(100,4,0.2) を使用している。次数系列(degree_sequence)は大きい順からソートしている。ソートしない場合には、degree_sequence = G.degree().values() と書く。kukan はヒストグラムの階層区間を指定している。histogram関数の変数で、density=Trueと指定しているのは、確率密度関数にするためである。plt.hist関数を用いて描くこともできるが、ここでは、より簡単なplt.plot関数を用いた。
このコードを実行すると、以下のグラフが描けます。
この例のスモールワールド・ネットワークの次数分布は以下の図に示される。 ワッツ=ストロガッツのモデルは現実のネットワークで観測される大きい群集化と短いパス距離に関する特徴を定式化することに成功しているが、現実の世界では、平均数よりもはるかに多いリンク数を持つノードが存在していることを説明できない。1999年、Barabasi and Albert(1999)は、平均数よりもはるかに多いリンク数を持つハブの存在を説明するモデルを提案するために、スケールフリー・ネットワークと呼ばれる理論を提案した。 イタリアの経済学者V・パレートは『政治経済学の原理(Cours d'economie politique)』(1897年)を発表し、その中で、パレート分布(80対20の法則)を提案した。統計量\(k\)のPareto分布は、累積分布形で\(F(k)=1-k^{-\gamma +1}\)と表現され、密度分布形では\(f(k)=(\gamma -1)k^{-\gamma}\)と表現される。例えば、エンドウ豆の収穫量の80%は20%のさやからもたらされる。イタリア国土の80%は人口の20%に所有されている。経済学におけるマーフィーの法則とも言える。収益の80%は従業員の20%があげている、顧客トラブルの80%は顧客の20%が持ち込んでいる、決定事項の80%は会議時間の20%内で処理されている、等々。 自然界に現れる多くの統計量の分布は釣り鐘型の形状を持つ。統計学の言葉でいえば、正規分布(normal distribution)に近い分布形をしている。身長の分布は150センチから190センチ内にほとんど収まり、その中にピークがある。しかし、ウェブ・ページが持つリンク数を調べたら、釣り鐘の形状をしていなかった。Albert, Jeong and Barabasi(1999)は、world wide web上のウェブ・ページのリンク数分布は冪乗則(power law distribution)に従うことを発見した。冪乗則(ベキ法則)の分布はリンク数\(k\)をもつウェブ・ページの数を\(N(k)\)とすると、\(N(k) \sim k^{-\gamma}\)と表現される。両対数グラフに表現すると、右下がりの直線になる。指数の値\(\gamma\)はその傾きの大きさになる。インカミング(in-coming)リンク数では、\(k \approx 2.1\)、アウトゴーイング(out-going)リンク数では、\(k \approx 2.5\)となっている事実が発見された。 Barabasi and Albert(1999)でも、ハリウッド俳優のリンク数もベキ法則に従うことも発見された。細胞内神経系も、\(k\)個の分子と相互作用する分子の数もベキ法則になっている。論文引用件数もベキ法則に従う。個々のネットワークは独自のベキ(冪)指数を持ち、その値は2から3になる。別の研究によれば、金融ネットワークの次数分布も冪乗則に従うことが知られている。ランダムネットワークとベキ法則に従うネットワークは、見た目も実際の構造も衝撃的に異なる。高速道路網にはハブは存在しないが、航空会社のルートマップを見れば明白になるように非常に多数の航空会社が乗り入れている空港がある。十数本の高速道路が合流する都市は存在しても、50本を越える高速道路を連結したハブの役割をする都市は存在しない。他方、米国での航空会社のルートマップには、シカゴ、ダラス、デンバー、アトランタなどのハブ空港が存在する。 ベキ法則の特徴は小さな事象が無数に存在すると同時に、一握りの極めて大きな事象が共存することである。鐘型の分布では、小さな事象は起こるが、非常に大きな事象は絶対に起こりえない。裾野は指数関数的に減少する。また、ベキ分布の特徴は、ピークが存在しない、平均的ノードがないことでもある。ネットワークを特徴づける平均などのスケール(尺度)が存在しない。だから、スケールフリー・ネットワークとも呼ばれる。ベキ法則に従うスケールフリー・ネットワークでは、少数のハブが存在し、そのハブがネットワークのトポロジーを基本的に決定する。ハブの登場と存在が、ネットワークの進化を支配する重要な組織原理になっている。 Barabasi and Albert(1999)は、ネットワーク形成の動的な過程を明示的にモデルに導入することによって、次数分布がべき乗則に従うことを示した。動的なリンク形成に関する第1の仮定は、新しいノードが生まれ、この新しいノードと既存のあるノードと間に新しいリンクが形成されるというネットワーク成長についての仮定である。第2の仮定は、新しいノードのリンク先の選択が、各既存ノードのそのときの影響力の大きさに偏向するようなメカニズムが働くという仮定である。この仮定を「優先的付着」(preferential attachment)の仮定という。豊かな人はより豊かになるというメカニズムを組み込むことに他ならない。 preferencial attachmentネットワークを描いてみよう。組み込み関数はbarabasi_albert_graph(p,m)を用いた。利用したプログラムは以下の通りです。 このコードを実行すると以下のグラフを表現します。 会社や組織の管理・運営、新商品の研究開発、大学のクラスやサークル、あるいは、趣味やスポーツの同好会など、様々な社会的経済的な活動を結節点として、現実社会での人間関係の人的ネットワークは形成されていく。私たちは、日常的に、人と人の間に形成された社会的なネットワークの中で日々の生活を送っている。ここで、ビクトル・ユーゴの小説『Les Miserables』における登場人物をノードとし、彼らの間の人間関係をリンクで結んで描いたネットワークを作成してみよう。networkx のモジュールを利用して以下のようなコードを書きます。 このコードを実行して描いたネットワークのグラフが下の図です。 人間関係の大きさに応じてリンク数が多くなる。当然のことながら、主人公のジャン・バルジャンとファンティーヌとその娘コゼットに接続するリンク数が最も多い。ノード番号11がValjean、ノード23がFantine、ノード26がCosetteに対応している。 最も基本的な意味で、ネットワークとは、ある対象物と他の対象物の組がリンクによって連結されているような対象物とリンンクの組合せの集合である。ソーシャル・ネットワークの例として必ず登場するのが、Zacharyによる大学空手倶楽部を通した学生間の友人関係のネットワークである。networkx のモジュールを利用して以下のようなコードを書きます。 このプログラムを実行すると、以下のグラフが得られます。 34名からなる友人ネットワークの中で、ノード番号0と33が最も多いリンク(友人)数を持つ。 以上の2例は networkX の公式サイトのこのページにあります。 以下の図は、1970年12月時点でのARPANET(Advanced Research Projects Agency Network)と呼ばれるコンピュータ・インターネットのネットワーク構造を描いたものである。ARPANETは1969年に米国国防総省の国防高等研究計画局のもとに構築された研究・調査のための大型汎用コンピュータのネットワークである。最初はカリフォルニア大学ロサンゼルス校 (UCLA)とスタンフォード研究所(SRI)との間で試験的に回線が引かれ、後に、UCLA、カリフォルニア大学サンタバーバラ校 (UCSB)、SRI、スタンフォード大学(STAN)、ユタ大学(UTAH)を結ぶ専用回線が敷設された。この ARPANET のネットワークのグラフを作成してみよう。 このプログラムを実行すると以下のようなグラフが描かれます。 各ノードはホスト・コンピュータが置かれている大学等を表現しており、リンクは各ホスト・コンピュータが専用回線で直接に接続していることを示す。ホスト・コンピュータを置く機関は、地理的には東海岸のマサチューセッツ工科大学(MIT)やハーバード大学(HARV)から西海岸のスタンフォード大学やUCLAなどの13大学等で、ネットワーク上では、リンクされた各ノード間の地理的距離はあまり関係がない。ちなみに、RAND研究所(RAND)はカリフォルニア州サンタモニカに位置するが、BBN社(BBN Technologies)はマサチューセッツ州ケンブリッジに位置する。このネットワークは情報通信ネットワークの典型例である。 1971年には、Interface Message Processor(IMP、現在のルーターに対応)として軽量なHoneywell 316が導入されて、ホストと最大63台のASCIIシリアル端末が接続された。1974年6月にはIMPが46台となり、1975年7月には57台のIMPが相互接続された。1981年までに213台のホストコンピュータが接続され、およそ20日に1台の割合で新たなホストが接続されるという状況になった。1983年、資金提供を行っていた国防省側の方針で、NCP(ネットワーク コントロール プログラム)をTCP/IP(Transmission Control Protocol /Internet Protocol )に切り換えることになり、ARPANETは初期のインターネットのサブネットとなった。これが今日のインターネットにおけるTCP/IPの使用にとって決定的な条件のひとつを作ったと考えられている。
次に、社会的ネットワークの分析例を取り上げましょう。社会的ネットワークのモデルについての解説は、このPDFファイル にあります。 networkX を用いて davis_southern_women_graph、Florentine families graphなどの社会的ネットワークを表現するソースコードは、networkX の公式サイトのこのページにあります。 15世紀イタリア・フィレンツェで Medici 家が強大な権力を維持できた理由について考察する方法として、当時のフィレンツェにおける有力な家系間のネットワークを取上げてみよう。この家系間ネットワークを確認するために、以下のようなプログラムを作成します。ノード番号5が Medici 家です。
このコード実行すると、下のグラフが得られます。 このネットワークにおいて、Networkxのアルゴリズム関数を用いて計算した詳細な結果は以下の表のようになります。betweenness_centrality 、 degree centality などのアルゴリズム関数については、この公式サイトを参照ください。 Medici家を含むこのネットワークで、betweenness cetrality(中継中心化度)及び degree centrality などの計算をしましょう。以下のような命令文を書けば、以下の結果が得られます。 この例における家系\(i\)と家系\(j\)を結びつける最短距離の経路の総数を\(P(i,j)\)と表記し、これらの経路の中に家系\(k\)が含まれている経路数を\(P_k(i,j)\)と表記する。Barbadori家とGuadagni家を結ぶ最短距離の経路は、3つのリンク(枝)を経由するBarbadori - Medici - Tornabuoni - Guadagniという経路とBarbadori - Medici - Albizzi - Guadagni の経路の2経路である。だから、\(i=\)Barbadori、\(j=\)Guadagniとしたとき、\(P(i,j)=2\)である。\(k=\)Mediciとすると、\(P_k(i,j)=2\)である。
\(k=\)Strozziとおくと \(P_k(i,j)=0\)、\(k=\)Albizziとおくと \(P_k(i,j)=1\)となる。Medici家はBardadori家とGuadagni家を結びつける上で中心的役割を果たす家系となっている。ネットワークにおけるこうした中心的役割を数量的に表現するのが、中継中心化度である。この計量化を活用すると、Medici家の係数は\(0.5219\)となる。つまり、Medici家以外の2家系を結ぶ最短経路総数のうち52%の経路はMedici家を経由していることがわかる。Strozzi家の中継集中度指数を計算すると、\(0.103\)となる。Medici家の次にこの値が大きい家系はGuadagni家で、その値は\(0.2545\)である。このことから、Medici家の政略結婚がネットワークの構築にいかに重要な役割をはたしたかを理解できる。 さらに、degree centralityの係数の値もMedici家が最大となっている。また、Medici家が最も多いリンク数6を持っています。社会的ネットワークにおける degree centrality や betweenness cetrality の定義は:このPDFファイル に掲載されています。 周知の通り、ネットワークの研究は、インターネット上での web のリンク接続、情報の交換と流通、イノベーションの伝搬、貿易取引と物流、金融資産の取引関係、友人関係、病気の伝染、生体内神経回路など、多種多領域にまたがる領域において急速に発展してきた。ネットワークは非常に多種多様な領域に広がっているが、大きく分けて4種類のネットワークに分類することができる。一つは、人々の生活に見られる社会的経済的なネットワーク (social and economic networks) である。会社関係、あるいは取引関係、同級生同士の人間関係、サークルを介した友人関係などから形成される人々のネットワークがこれに対応する。企業と企業間の取引関係のような、組織と組織間のネットワークもこれに入る。最近では、Facebook、Twitter, LINE などの SNS を介した新しい人的ネットワークが形成されている。 次は、インターネット社会の基盤を形成する情報ネットワーク (information networks) である。E メールの連鎖のネットワーク、学術論文の引用ネットワークやインターネット上において各 web ページのドキュメントがハイパーリンクされているなど、情報を対象物として連結されたネットワークである。 三つ目に、経済的活動のインフラを提供するネットワークとして、財やサービスの流通を行うために計画された技術的ネットワーク (technological networks) に分類されるものがある。代表的なものとして、各ドメイ ン間をつなぐインターネット回線、電力配電網、運輸交通網のようなインフラ的なネットワークである。 最後に、生物学的ネットワーク (biological networks) をあげることができる。生体内におけるニューロン 神経のネットワーク、生態系における植物連鎖のネットワーク、病原菌の拡散過程を研究するときに採用され る生体間の接触ネットワークなどが、これに当たる。 近年における情報通信技術の驚異的な進歩は社会的ネットワークの性質に大きな影響を与えている。20世紀初頭以来、急速に、世界は小さくなっている。インターネットの進歩によりさらに世界は小さくなり続けている。多数の人々は新しいSNSを介して比較的に少人数グループとの間で情報通信を行っている。政治的なブログに見られるように、新しいSNSの発達は各個人がより多様な意見を持つようになることを必ずしも保証しない。多分、SNSの進展は、他者の行動や意見を過剰に模倣する烏合の衆、群衆化を急速に作り出す可能性を持つ。Facebook、Twitter、LINEに代表される新しいSNSは人々が入手する情報の性質を変化させたり、情報の処理方法を変化させるでしょう。 社会経済ネットワークはそれを構成するノード(結節点)が人間あるいは人的組織であり、人間あるいは人的組織の意思決定がネットワーク上で相互関係している点に特徴がある。だから、社会経済ネットワークの重要な特徴は、ネットワーク内のリンク接続の構造に依存するだけでなく、ネットワーク構造上で起きる行為の相互干渉の性格にも大きく依存する。ネットワーク内の各主体あるいは組織の意思決定はネットワーク上で相互依存するので、社会経済ネットワークの分析ではゲーム理論の枠組みが必要となってくる。ネットワーク内の各主体あるいは組織の意思決定が他の主体に影響を持たらす現象を情報カスケード現象やネットワーク効果と呼んでいる。このような情報カスケード、群集化、ネットワーク効果がどのようなメカニズムで働き、どのような社会的現象を引き起こすのかを理解する必要がある。 ここでは、イノベーションの波及問題をネットワークモデルを用いて分析してみましょう。この理論的な解説はこのPDFファイル を参照して下さい。 興味のある方は以下の論文を読んでみて下さい。大学教養程度の数学が必要です。 ネットワークの理論入門:このPDFファイル ネットワークの理論.母関数アプローチ:このPDFファイル 経済的ネットワークのモデルについての解説:このPDFファイル 社会的ネットワークのモデルについての解説は:このPDFファイル 銀行間ネットワークの解説:このPDFファイル 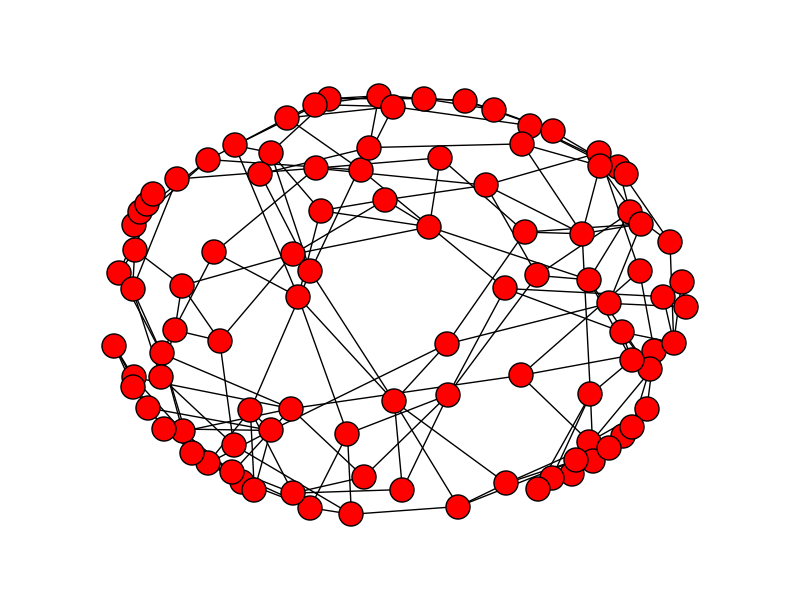
# Barabasi Albert graph
try:
import matplotlib.pyplot as plt
except:
raise
import networkx as nx
G=nx.barabasi_albert_graph(100,2)
plt.figure(1)
nx.draw(G) #nx.draw_random(G)
plt.savefig("B_A.png") # save as png
plt.show()
degree_sequence=sorted(G.degree(),reverse=True) # degree sequence
#print "Degree sequence", degree_sequence
# the histogram of the data
print("degree sequence =", degree_sequence)
import numpy as np
kukan=range(0,22)
hist, kukan=np.histogram(degree_sequence,kukan,density=True)
x=range(0,20)
print(hist,kukan)
plt.plot(hist)
plt.xlabel('degree')
plt.ylabel('frequency')
plt.title('degree frequency(Barabasi_Albert: n=100, m=2)')
plt.grid(True)
#plt.xlabel("rank")
plt.savefig('BA_degree.png')
plt.show()
Barabasi_Albert型ネットワークの次数分布は以下の通りである。 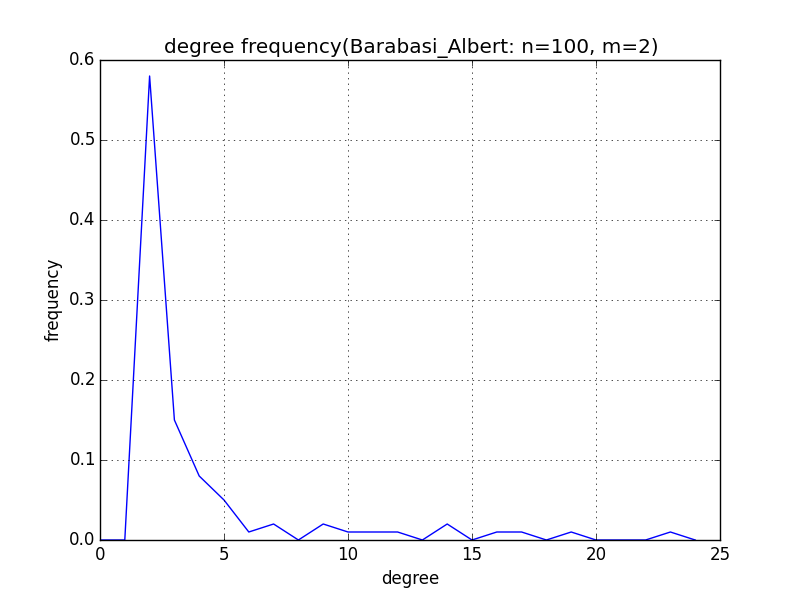
社会的ネットワークの代表例
"""
References
.. D. E. Knuth, 1993.
The Stanford GraphBase: a platform for combinatorial computing,
pp. 74-87. New York: AcM Press.
"""
import networkx as nx
H = nx.Graph()
import matplotlib.pyplot as plt
#H=nx.read_gml('lesmiserables.gml')
H=nx.les_miserables_graph()
nx.draw(H, with_labels=True,node_size=200, node_color='b', font_color='y')
plt.axis('off')
plt.title('Les Miserables')
plt.savefig("lesmiserables.png") # save as png
plt.show()
print("Node Degree")
for v in H:
print(f"{v:4} {H.degree(v):6}")
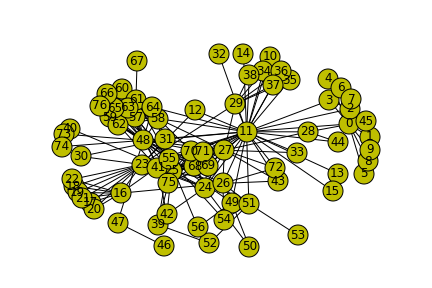
『Les Miserables』における人間関係
"""
Zachary's Karate Club graph
Data file from: http://vlado.fmf.uni-lj.si/pub/networks/data/Ucinet/UciData.htm
Zachary W. (1977). An information flow model for conflict and fission in small groups. Journal of Anthropological Research, 33, 452-473.
"""
import matplotlib.pyplot as plt
import networkx as nx
G = nx.karate_club_graph()
print("Node Degree")
for v in G:
print(f"{v:4} {G.degree(v):6}")
plt.axis('off')
plt.title('karate_club')
nx.draw_spring(G, with_labels=True, node_color='y')
plt.savefig("karate_club.png") # save as png
plt.show()
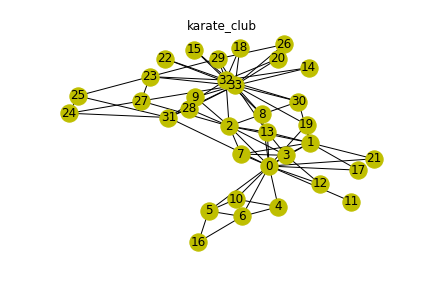
空手クラブを介した友人関係
# creating a new network
import networkx as nx
G = nx.Graph()
N=['UCLA','UCSB','SRI', 'STAN', 'RAND', 'UTAH','MIT','BBN', 'HARV','CASE', 'CARN','LINC']
E=[('UCLA','UCSB'),('UCLA','SRI'),('UCLA','STAN'),('UCLA','RAND'),('SDR','RAND'),('SRI','UCSB'),('SRI','STAN'),('SRI','UTAH'),('UTAH','SDR'),('UTAH','MIT'),('RAND','BBN'),('MIT','LINC'),('MIT','BBN'),('BBN','HARV'),('LINC','CASE'),('HARV','CARN'),('CASE','CARN')]
G.add_nodes_from(N)
G.add_edges_from(E)
# drawing the created network
import matplotlib.pyplot as plt
nx.draw(G,with_labels=True, node_color='y')
plt.axis('off')
plt.title('an example')
plt.savefig("ARPANET.png") # save as png
plt.show()
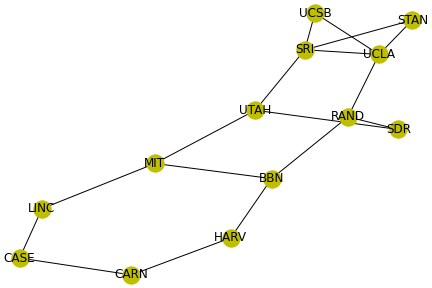
1970年12月でのARPANETネットワーク
社会的ネットワークの分析:アルゴリズム関数
# Watts Strogatz graph
import matplotlib.pyplot as plt
import networkx as nx
G = nx.Graph() # or DiGraph, MultiGraph, MultiDiGraph, etc >>> G = nx.Graph(name='my graph')
nod=range(0,15)
e= [(3,5), (4,5), (5,10),(5,11),(5,13), (5,6) ] # list of edges
G.add_nodes_from(nod)
G = nx.Graph(e)
e1=[(0,1),(0,2), (0,4),(1,4), (1,7),(1,2), (2,3),(3,6),(11,12), (13,14),(6,8),(8,13), (8,9),(13,14)]
G.add_edges_from(e1)
pos=nx.spring_layout(G) # positions for all nodes
# nodes
nx.draw_networkx_nodes(G,pos,
nodelist=[0,1,2,4,7,8,9,10,12,14],
node_color='b',
node_size=30,
alpha=0.8)
nx.draw_networkx_nodes(G,pos,
nodelist=[3,4,5,6,10,11,13],
node_color='r',
node_size=50,
alpha=0.8)
# edges
nx.draw_networkx_edges(G,pos,width=1.0,alpha=0.5)
nx.draw_networkx_edges(G,pos,edgelist= e, width=1.5,alpha=0.5,edge_color='r')
nx.draw_networkx_edges(G,pos,edgelist= e1, width=1.5,alpha=0.5,edge_color='b')
# some math labels
labels={}
labels[0]= 'Castellan'
labels[1]='Peruzzi'
labels[2]='Strozzi'
labels[3]='Ridolfi'
labels[4]='Barbadori'
labels[5]='Medici'
labels[6]='Tornabuorn'
labels[7]='Bischeri'
labels[8]='Guadagni'
labels[9]='Lambertertes'
labels[10]= 'Acciaiuol'
labels[11]='Salviati'
labels[12]='Pazzi'
labels[13]='Albizzi'
labels[14]='Ginori'
# cumputing the measures of network
print('the clustering coefficient for nodes = ',nx.clustering(G))
print('degeree sequence = ',G.degree())
print('degree histogram = ', nx.degree_histogram(G))
print('degree centrality = ',nx.degree_centrality(G))
print('betweenness centrality = ', nx.betweenness_centrality(G))
#nx.draw_spring(G)
nx.draw_networkx_labels(G,pos,labels,font_size=12)
plt.axis('off')
plt.title('Fifteen-century Florentine marriages network')
plt.savefig("medici.png") # save as png
plt.show()

print('the clustering coefficient for nodes = ',nx.clustering(G))
print('degeree sequence = ',G.degree().values())
print('degree histogram = ', nx.degree_histogram(G))
print('degree centrality = ',nx.degree_centrality(G))
print('betweenness centrality = ', nx.betweenness_centrality(G))
{フィレンツェにおける家系ネットワークの例}
family clustering degree sequence degree centrality betweenness centrality
'Castellani' 0.6666 3 0.2142 0.0549
'Peruzzi' 0.6666 3 0.2142 0.0219
'Strozzi' 0.3333 3 0.2142 0.1025
'Ridolfi' 0.3333 3 0.2142 0.1135
'Barbadori' 0.3333 3 0.2142 0.0934
'Medici' 0.0666 6 0.4285 0.5219
'Tornabuoni' 0.3333 3 0.2142 0.0915
'Bischeri' 0.0 1 0.0714 0.1043
'Guadagni' 0.0 4 0.2857 0.2545
'Lamberteschi' 0.0 1 0.0714 0.0
'Acciaiuoli' 0.0 1 0.0714 0.0
'Salviati' 0.0 2 0.1428 0.1428
'Pazzi' 0.0 1 0.0714 0.0
'Albizzi' 0.0 3 0.2142 0.2124
'Ginori' 0.0 1 0.0714 0.0
イノベーションの波及モデル
[ 続く]