|
急激なコンピュータ技術の発達により人口知能(AI)技術がロボットや自動車の安全運転、スマホによる自然言語や音声の認識、フィンテック、さらにはIoTのインフラ技術などに応用されるようになってきました。さらには、ChatGPT、 Claude、や Gemini などに代表される生成AI(Generative AI)が登場し、テキストや画像、動画など、さまざまなコンテンツを生成することが出来るようにようになってきました。現在では、AIは日常生活のあらゆる場面で利用されています。
人工知能(AI)技術の基礎は深層学習(deep learning)と言われる分野での研究開発に多くを負っています。深層学習も機械学習(machine learning)の一つの分野であり、または大量のデータを用いてパラメータの学習をするという意味では、データサイエンスと呼ばれている分野における研究にも属します。このページでは AI の基礎をなす深層学習及び機械学習とは何を目指しているのか、いかなる概念のもとで、どのような構造を持つものかを学びたいと思います。
機械学習の分野の中でニューラルネットワークという概念を基にしてコンピュータビジョンや自然言語処理などに関わる学習アルゴリズムを開発する領域がデープラーニングに対応すると考えます。まずは、ニューラルネットワークという概念について学習するところから始めます。機械学習及びディープラーニングの多くのフレームワークはPython及びC++で記述されています。ニューラルネットワークの基本的構造とその実装を理解するための言語としてはPythonが理解できれば十分でしょう。そういう意味では、この領域において必須のプログラミング言語はPythonです。したがって、読者の皆さんもPythonの基礎的な知識を習得していると想定します。Python の知識がない方は、このPython 入門のページをお読みください。他方、LinuxやC言語の知識は想定していません。
ビッグデータとニューラルネットワークの大規模化に伴って、大量の学習演算をすることが必要となってきました。現実的なディープラーニングのソフトを実装して学習を行わせるためには通常のCPUを搭載したコンピュータでは心もとないのが現実です。ディープラーニングのフレームワークの多くはGPU(graphics Processing Unit)をサポートしています。複数のGPUや複数台のCPUマシンを用いた分散学習も必要となっています。ましてや、生成AIの利用や開発においては、データセンターと呼ばれる膨大なコンピュータ資源が必須です。しかし、このページでは、シンプルな認識系AIについてのみ学習するので、CPUを搭載した普通のPCを使用することを前提にしています。OSはLinuxでも、MacOSでもWindowsでも、Python環境がインストールされていれば十分です。
このページで利用されるPython3のスクリプトなどのコードはすべて、私のGitHubにありますので、そこからダウンロードして、利用してください。GitHubとは、ソフトウエア開発プロジェクトのためのweb上でのソース管理サービスのことで、GitHubのトップページにアクセスして、アカウントを登録すれば、無料で利用できます。また、今では、pythonを使用する上で必須の環境になっているJupyter Notebookを使用します。Jupyter notebook のインストールが完了していない場合には、このJupyter Notebookのページを読んでください。Jupyter Notebookの簡単な使用法も説明しています。
なお、GoogleがGoogle Colaboratory という無料で使用できるCloud サービスを開始しました。Google Colaboratoryは、Jupyter Notebook をベースとした、Googleの仮想マシン上で動くPython実行環境です。無料であり、Googleにアカウントを登録すれば、Pythonなどのインストール等の作業に手間を取られることなく、すぐに機械学習のコードを実行することができます。GPUも無料で利用することができるので、GPUコンピューティングによる機械学習やDeep Learning等の高速化処理も可能です。Pythonの基礎的な知識があれば、スマホからでも実習ができます。このページでも、Google Colabで実習できるノートブックを作成して、Google Colabにアップロードしていますので、Python環境をセットアップできない方やスマホから実行したい方は是非利用して下さい。
AIや機械学習に関するページで説明されるPython コードを自分の手で実行したいと希望する方は、Googleのアカウント登録、および、GitHubのアカウント登録をすることをお勧めします。両方とも無料で行えます。
Deep Learning のオーソドックスなテキストブックは、"Deep Learning "(Adaptive Computation and Machine Learning series) by Ian Goodfellow , Yoshua Bengio , and Aaron Courville (MIT Press ) 2016/11/10 です。これを読みこなすには、数学理解とかなりの忍耐が必要です。Pythonでの実装については触れていません。Deep Learning の Python 実装を兼ねた参考書の代表的なものは以下の通りです。
この中で、1.と2.はPython API を使用せずに Python 実装をすることを目指しています。Python の初心者には、1.の方が読みやすいと思います。3. はDeep Learning の広い範囲をカバーしていますが、 Keras + Tensorflow を使用しています。この故に、2017年時点で書かれた付属のコードでは、Keras が Tensorflow のモジュールに統合されたことに伴い、Tensorflow 2.x ではエラーが出ますので、修正が必要です。
ご質問、コメントなどは こちらからメール送信して下さい。
Last updated: 2026.1.10(first uploaded 2018.1.21)
パーセプトロン・モデル |
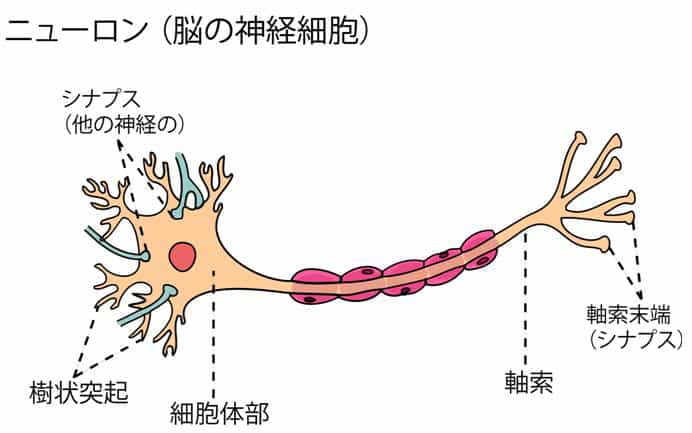
最初に、パーセプトロンと呼ばれるモデルについて説明します。パーセプトロンとは最も単純な情報の処理過程のモデルで、複数の入力信号(情報)を受け取って、その情報を加工して出力を送り出すゲート・モデルのことです。このパーセプトロンというモデルはニューロンの情報処理過程を簡単化したモデルから出ています。

人間の神経細胞ニューロンの構造とパーセプトロンの関係を見てみるとよく分かります。ニューロン樹状突起に入る信号がパーセプトロンの入力信号で、軸索(末端シナプス)が出力に対応しています。情報を処理する細胞体がパーセプトロンのノードの部分になります。
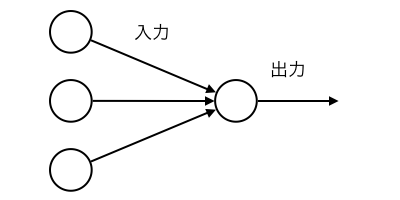
このグラフでは入力数が3になっていますが、実際には、入力の数も樹状突起の数だけありますので、制限はありません。出力信号の数もシナプスの数だけあるので、複数個あることが想定できます。ここでの最も簡単なパーセプトロンのモデルは入力信号が2種類で、出力信号が一つです。
入力信号が\( (x_1, x_2) \) であり、各入力信号に対する重みが\( (w_1, w_2) \)であるとして、出力信号を\( y \)とします。\( u \)が以下のように重み\( w \)をつけて荷重計算されると仮定します。
\[ u = w_1 x_1 + w_2 x_2 \]このとき、
\( u \le \theta \)なら、出力信号を \( y = 0 \)とし、ような処理がされるとします。これが単純な入力層と出力層の2層からなる2層型パーセプトロンと呼ばれるモデルです。ここで、\( \theta \)は閾値と呼ばれるパラメータです。入力信号の荷重和がこの閾値を超えると、ゲートが発火するというものです。これを関数形で表現すると
\[ y = f(u) = \begin{cases} 1 & \text{if } u= w_1 x_1 + w_2 x_2 > \theta \\ 0 & \text{if } u= w_1 x_1 + w_2 x_2 \le \theta \end{cases} \]となります。このステップ関数は活性化(activation)と呼ばれる役割をします。だから、この関数は活性化関数と呼ばれます。
最もシンプルな2層型パーセプトロンとして、AND型、OR型、NAND型という3種類の処理ゲートが想定されます。AND型は以下の表のような入・出力関係になるケースです。これを真理値表と言います。
| \(x_1\) | \(x_2\) | \(y\) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
これは2入力がともに1の時にのみ1を出力して、それ以外の時はゼロと出力するゲートです。パラメータ値をどのように設定すればAND型ゲートが作成できるでしょうか。
\[ (w_1, w_2, \theta) = (1.0, 1.0, 1.0) \] とするとき、AND型になります。 \[ (w_1, w_2, \theta) = (0.5, 0.5, 0.5) \]とする場合にも、AND型ゲートが成り立ちます。
次に、NAND型モデルをとりあげます。真理値表は以下の通りです。
| \(x_1\) | \(x_2\) | \(y\) |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
例えば、パラメータ値を
\[ (w_1, w_2, \theta) = (-0.5, -0.5, -1.0) \]と設定すると、NAND型ゲートが作成できます。
次に、OR型ゲートを考えましょう。これは2つの信号のうちどちらかが1であれば、出力を1とするモデルです。以下に真理値表を書きます。
| \(x_1\) | \(x_2\) | \(y\) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
このOR型ゲートを実現するパラメータ値はどうなるでしょうか。すぐ解ると思いますが、例えば、
\[ (w_1, w_2, \theta) = (1.0, 1.0, 0.5) \]のケースで考えてみてください。
以上のことから、パーセプトロンという概念を使用すると、パラメータ値を色々と変えることによりAND型、NAND型、OR型ゲートをそれぞれ実現することがわかりました。そこで、これらのモデルをPythonのコードで実装することを考えましょう。以下にAND型ゲートを組み込むPythonスクリプトを示します。
# coding: utf-8
# AND_gate.py
import numpy as np
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
theta = 0.5
s = np.sum(w*x) - theta
if s <= 0:
return 0
else:
return 1
if __name__ == '__main__':
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = AND(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
新しくディレクトリ(例えば、perceptron)を作成して、このコードをAND_gate.pyという名前で保存してください。このファイルをPythonで開いて、実行してください。真理値表の通りの結果が表示されるはずです。
パーセプトロンの各パラメータ値を変えると、AND、OR、NAND型になるので、Pythonのスクリプト上でパラメータ値を入力変数に設定しておけば汎用のゲート・モデルが記述できます。以下のスクリプトを見てください。
#coding: utf-8
# OR_gate.py
import numpy as np
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([1.0, 1.0])
theta = 0.5
s = np.sum(w*x) - theta
if s <= 0:
return 0
else:
return 1
if __name__ == '__main__':
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = OR(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
このスクリプトをOR_gate.pyという名前のファイルでディレクトリ(perceptron)に保存してください。更に、以下のスクリプトをNAND_gate.pyという名前でディレクトリ(perceptron)に保存してください。
#coding: utf-8
# NAND_gate.py
import numpy as np
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
theta = -1.0
s = np.sum(w*x) - theta
if s <= 0:
return 0
else:
return 1
if __name__ == '__main__':
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = NAND(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
これらのスクリプトを実行すると、各パーセプトロンの真理値を表示します。以上のパーセプトロンでは、出力値をゼロとする入力信号と1とする入力値の範囲が直線の上側か、下側かで識別できます。線形性を持つと言います。
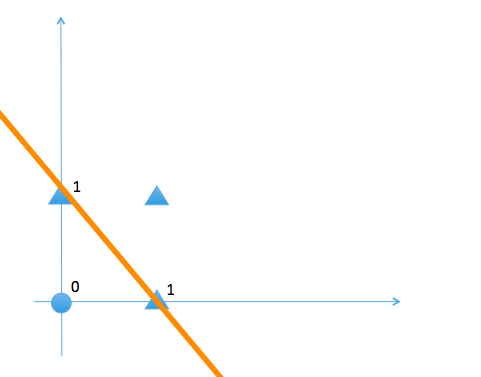
次に、排他的論理和と呼ばれるゲートモデル、XORゲートを取り上げます。XORゲートは2入力信号のうちどちらか一つの信号のみが1であるときにのみ出力を1とし、それ以外の場合にはゼロを出力する。真理値表は以下のようになります。
| \(x_1\) | \(x_2\) | \(y\) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
このXORゲートは単純なパーセプトロンでは実現できない。その理由はXORゲートが線形性を持たないからです。言い換えると、出力の値をゼロとする入力信号と1 とする入力信号の範囲が直線の上側か、下側かで差別化できないからです。実はXOR回路はNANDゲート、ORゲートおよびANDゲートを繋ぎ合わせることで合成できます。NANDゲートの出力とORゲートの出力を\( (s_1, s_2) \) とするとき、XORゲートの真理値を書き直すと以下のようになる。
| \(x_1\) | \(x_2\) | \(s_1\) | \(s_2\) | \(y\) |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
NANDゲートの出力の値とORゲートの出力の値を入力信号とするANDゲートの論理回路を通せば、XORの真理値を出力することができます。これをPythonスクリプトで実現する。
# coding: utf-8
# XOR_gate.py
from AND_gate import AND
from OR_gate import OR
from NAND_gate import NAND
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
if __name__ == '__main__':
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = XOR(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
このスクリプトをファイル名 XOR_gate.pyとしてディレクトリ(perceptron)に保存してください。上記のPythonスクリプトはすべて同一のディレクトリ(名称は適当でいいです)に保存してください。読み込まれるPythonモジュールはNumPy、AND_gate.py、OR_gate.py、NAND_gate.pyです。上記のコードはこのColabから実行できます。
このXORゲートは3層からなるパーセプトロンとなっています。第1層と第2層の間にNAND型論理回路とOR型論理回路が組み込まれ、それらの出力がAND型論理回路で処理されて第3層に出力されている。最も左側の層を入力層、最も右側を出力層と呼び、それらに挟まれた第2層目を中間(隠れ)層と呼びます。こうして、パーセプトロンを多層に組み合わせると、非線形の識別が可能となります。ニューラルネットワークはこれらの多様なパーセプトロンが多数の層になって形成されます。言い換えると、ニューラルネットワークは非線形性の識別能力を持つデータ処理回路となります。
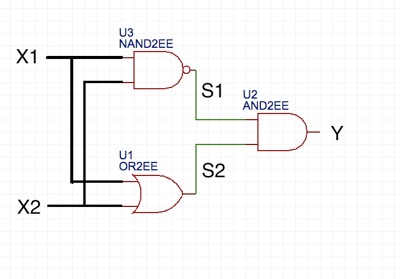
XORゲートの模型図
単純なニューラルネットワーク:アヤメの品種識別 |
ニューラルネットワークの話に入る前に、ここで、個別パーセプトロンの数式表現を整理します。 以下に一般的な入力シグナルを持つパーセプトロンの図が描かれています。通常、出力信号の数は一般的にm個あると想定されます。このグラフでは 出力シグナルは1つになっています。
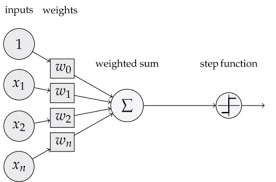
出力信号数が一つのケース
出力信号はstep function(ステップ関数)を通して出力されています。上で説明されている通り、このステップ関数をパーセプトロンの説明では活性化関数(activation function)と呼びます。ステップ関数を含めて、活性化関数として用いられる関数型にはsoftmax関数、sigmoid関数と言われるものがあります。(後で、説明します。)一般的に、活性化関数を
\[ \phi(z) \]と表現します。ステップ関数の値が(0,1)のケースや(-1,1)のケースもあります。活性化の閾値を\( \theta \)とすると、ステップ関数の値が(-1,1)のケースでは以下の通りに表記されます。
\[ \phi(z) = \begin{cases} 1 & \text{if } z = w_1 x_1 + w_2 x_2 + ... + w_n x_n - \theta > 0 \\ -1 & \text{if } z = w_1 x_1 + w_2 x_2 + ... + w_n x_n - \theta \le 0 \end{cases} \]パーセプトロンへの入力信号の荷重和\( z \)は\( w_0 = - \theta \)と置くと、一般的に
\[ z= w_0 + w_1 x_1 + w_2 x_2 + ... + w_n x_n \]と表現されます。パーセプトロンの出力\(y\)は活性化関数を通して、一般的な表現としては
\[ y =\phi(z) \]と表現します。通常、出力信号の数は一般的に複数個あると想定されますが、簡単化のために、ここでは一つとしています。
閾値に対応する部分はバイアスユニットとも言われます。バイアスユニットからの信号も通常の入力と同列に取り扱うために、
\[ x_0 = 1 \] と置きます。入力信号の数が一般的に\(n\)個ある場合の入力信号ベクトル\(x\)を、バイアスユニットの分を加えて \[ x = (x_0, x_1, x_2, ..., x_n) \] と表現します。各入力信号に対する重み\(w\)が \[ w =(w_0, w_1, w_2, ..., w_n) \]であるとします。信号ベクトルと重みベクトルは、バイアスユニットの分だけ要素数が+1されます。入力信号の荷重値\(z\)は以下のように計算される。
\[ z = w_0 x_0 + w_1 x_1 + w_2 x_2 + ... + w_n x_n \]以下、同様です。ただし、Pythonの実装では、バイアスユニットからの信号を一般の入力信号から区別して、\( b = w_0x_0 \) と表現するケースもあります。
最も単純なパーセプトロン・モデルを用いた重みパラメータの推定問題を見てみましょう。Rozenblattが提案した手法を用いて、パーセプトロンの重みwの値を推定します。この課題に応えるために用意されたデータの一つにiris(アヤメ)データセットがあります。これは3種類のアヤメ(iris setosa, iris versicolor, iris virginica)について、4つの特徴に関するデータ150個を収集したもです。アヤメの花びらについて知らない読者もいると思われますので、下にアヤメの写真を掲載します。

このアヤメのデータセットは、UCI Machine Learning Repositoryから、Pythonのpandasライブラリーを使用して直接読み込むことができます。以下のコードを、jupyter notebookからPythonシェルで実行すると
import pandas as pd
df = pd.read_csv('https://archive.ics.uci.edu/ml/'
'machine-learning-databases/iris/iris.data', header=None)
df.tail()
以下の結果が表示されます。
out [1]:
0 1 2 3 4
145 6.7 3.0 5.2 2.3 Iris-virginica
146 6.3 2.5 5.0 1.9 Iris-virginica
147 6.5 3.0 5.2 2.0 Iris-virginica
148 6.2 3.4 5.4 2.3 Iris-virginica
149 5.9 3.0 5.1 1.8 Iris-virginica
この出力はデータの最後の5個のサンプルを表示しています。列番号0はがく(sepal、外花被片)の長さ、列番号1はがくの幅、列番号3、4は花びら(petal、内花被片)の長さと幅のデータです。第1列目の数字はサンプル数です。
アヤメのsetosa種とversicolor種のデータだけを整理します。以下のコードをjupyter notebookでコピペします。
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
# select setosa and versicolor
y = df.iloc[0:100, 4].values
y = np.where(y == 'Iris-setosa', -1, 1)
# extract sepal length and petal length
X = df.iloc[0:100, [0, 2]].values
# plot data
plt.scatter(X[:50, 0], X[:50, 1],
color='red', marker='o', label='setosa')
plt.scatter(X[50:100, 0], X[50:100, 1],
color='blue', marker='x', label='versicolor')
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left')
plt.tight_layout()
#plt.savefig('./images/02_06.png', dpi=300)
plt.show()
sepalとpetalのデータを横軸、縦軸とする散布図が描かれます。下の図を参照してください。
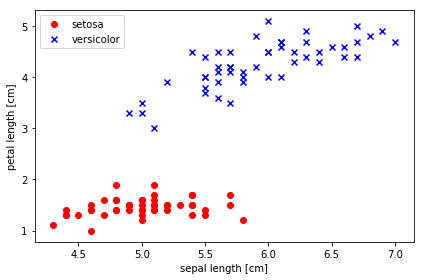
y = df.iloc[0:100, 4].values は、配列変数dfの中から、0行から100行未満までと、4列のデータの値(values)を変数yに入れること指示します。上で見たように、データの4列目にはアヤメの種の名前が入っています。y = np.where(y == 'Iris-setosa', -1, 1) は、要素の値が'Iris-setosa' である場合は、-1 に変更し、そうでない場合は1 を代入するという条件操作を意味します。この結果、教師ラベルの変数yの要素値は-1と1だけに変更されます。X = df.iloc[0:100, [0, 2]].values により、変数Xにはdf の1列目、3列目(df[0:100,[0,2]])の特徴データ(sepal length、petal length)の値が格納されます。# plot data 以下が散布図を描くpltの部分です。
Sebastian Raschka氏が学習用のモデルとコードを提供していますので、それを利用します。ソースは、私のGitHubのiris_Perceptron.ipynbをダウンロードしてください。Colabで実行できるノートブックはこちらです。
Sebastian Raschka氏が提供したミニバッチ学習用のperceptron モデルのコードを下に示します。Rozenblattによるパーセプトロンの学習規則は単純です。
1. 重みを0または小さな値で初期化する。
2. 訓練サンプルごとに以下の手順を繰り返す。
⑴出力値を計算する。
⑵正解と出力値の差に学習率を乗じて、重みを更新する。
import numpy as np
class Perceptron(object):
def __init__(self, eta=0.01, n_iter=10):
self.eta = eta
self.n_iter = n_iter
def fit(self, X, y):
self.w_ = np.zeros(1 + X.shape[1])
self.errors_ = []
for _ in range(self.n_iter):
errors = 0
for xi, target in zip(X, y):
update = self.eta * (target - self.predict(xi))
self.w_[1:] += update * xi
self.w_[0] += update
errors += int(update != 0.0)
self.errors_.append(errors)
return self
def net_input(self, X):
"""Calculate net input"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def predict(self, X):
"""Return class label after unit step"""
return np.where(self.net_input(X) >= 0.0, 1, -1)
このコードでは、perceptron という名前のクラスを定義して、このクラス内のメソッドとして、__init__、fit、net_input、predict の4つが定義されています。マーク""" ... """ の間はコメント文です。メソッド fit で重みの学習が行われます。このモデルを学習させる時は、学習率eta=0.1、学習回数 n_iter=10 のケースでは
ppn = Perceptron(eta=0.1, n_iter=10) ppn.fit(X, y)
と入力して、使用します。ppn.fitで、エポック毎の識別間違いの数(ppn.errors_)が返されます。python コードの理解に難解な箇所があるかもしれませんが、まずは、プログラムを実行して見てください。
Jupyter Notebookを起動して、Iris_Perceptron.ipynbを開いてください。この Google Colabからでも実行できます。このnotebookを上から順番に実行すると、以下のような結果が得られます。訓練したモデルに基づいて、予測されたパラメータ値から計算したモデルの識別予測直線と散布図を描くと下のようになります。図中の直線がパーセプトロンで予測される識別境界です。四角の点がアヤメのsetosa種、×の点がversicolor種に対応します。
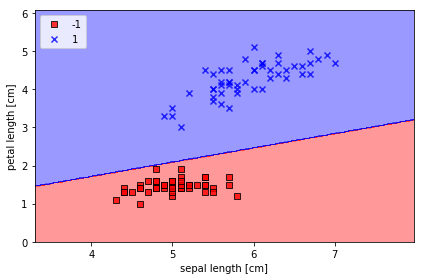
アヤメのsetosa種とvergicolor種の散布図
詳細な出力の手続きやPythonスクリプトについては、私のGitHubのリポジトリを参照してください。パーセプトロンの学習アルゴリズムの改良型であるADALINE(ADaptive LInear NEuron)を用いて重みの学習をすると、より優れた識別ができることが知られています。ここでは触れません。上図の識別直線が上方に少し移動することが確かめられます。ただし、3つの品種を線形直線で識別することは不可能です。これが単純パーセプトロン・モデルの限界です。
活性化関数として採用されるものはステップ関数だけではありません。これから取り上げるニューラルネットワークで重要な活性化関数の一つはシグモイド関数(sigmoid function)と呼ばれる関数です。この関数は、経済学など(広告やイノベーション伝搬)ではロジスティク曲線(logistic curve)と呼ばれています。シグモイド関数(ロジスティク曲線)は
\[ \phi(z) = \frac{1}{1+exp(-z)} \]と表現されます。ここで、\(exp(x)\)は指数関数です。シグモイド関数とステップ関数のグラフは下図のように比較できます。
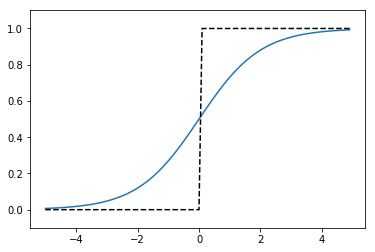
シグモイド関数(実線)とステップ関数(破線)のグラフ
シグモイド関数のグラフは連続的に変化してなめらかですが、ステップ関数のグラフは原点でジャンプします。また、シグモイド関数は入力の値が大きくなるに連れて、限りなく1の値に漸近します。両者の共通点は関数値がゼロと1の間に収まることです。
さらに、活性化関数として用いられる関数形として、以下に定義されるLeLU(Rectified Linear Unit)関数が使用されます。
\[ \phi(z) = \begin{cases} z & \text{if } z > 0 \\ 0 & \text{if } z \le 0 \end{cases} \]最後に、softmax関数を取り上げます。softmax関数は出力層からの出力信号が複数となるケースに採用される関数です。エントロピー関数を土台として、ロジスティック関数を一般化したものです。以下のように定義されます。出力層がn個の入力信号から構成され、i番目の入力信号を\(a_i\)とするとき、k番目の出力\(y_k\)は
\[ y_k = \frac{exp(a_k)}{\Sigma_{i=1}^n exp(a_i)} \]に従って計算される。このsoftmax関数による処理は各出力に確率分布を与えるもので、分類問題に利用されます。Pythonに実装すると以下のようになります。
# coding: utf-8
# softmax.py
import numpy as np
def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y=exp_a/sum_exp_a
return y
if __name__ == '__main__':
a = np.array([1.0, 2.0, 3.0])
y=softmax(a)
print(y)
exp(a)が非常に大きな数値になることを避けるためのオーバーフローに対する処理をする必要もあります。詳しくは、斎藤康毅著『ゼロから作るDeep Learning』(オライリー・ジャパン社)などの参考書を参照してください。
多層パーセプトロン:手書き数字の画像識別 |
ここからは、多層パーセプトロン、つまり、ニューラルネットワークと呼ばれる人工知能で必須の道具立てを取り上げます。行列の積の計算を頻繁に取り扱いますので、Pythonスクリプトでどのように記述するのか説明します。Pythonシェルで以下を実行してください。
>>>import numpy as np
>>>A = np.array( [[1,2],[3,4]] )
>>>B = np.array( [[5,6,7],[8,9,10]])
>>>C = np.dot(A, B)
>>>print(C)
[[21, 24, 27],
[47, 54, 61]]
dot(A,B)は線形代数での行列の積A・Bを計算します。AとBがベクトルの場合はベクトルの内積を計算します。(注意:MATLABなどでの命令文と異なります。)
多層パーセプトロンの例を取り上げます。下図を見てください。3層パーセプトロンと4層パーセプトロンの例が描かれています。
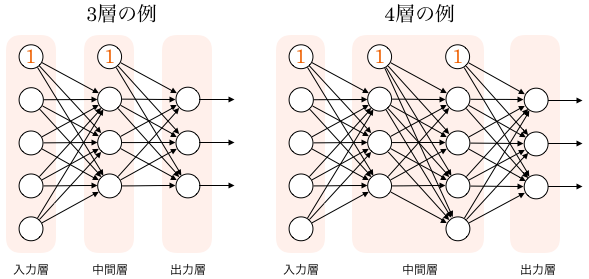
3、4層パーセプトロンの例
入力層(第1層)から第2層(中間層、hidden layer)へは5つの信号が入ります。出力層の出力は3つになっています。上端に位置するノード①は閾値を表現するためのもので、実際には存在しないニューロンで、便宜上から表示され、バイアスノードと呼ばれます。
バイアスユニットからの信号を通常の入力信号とは区別して
\[ b = w_0 \] と表記するときは、入力の荷重和は \[ z =w_1 x_1 + w_2 x_2 + ... + w_m x_m + b \]という計算になります。
いま、k番目の層のi番目のノードの出力信号を\( a_i^{(k)} \)と表記する。第1層(入力層)の出力信号ベクトルは
\[ a^{(1)}= \begin{bmatrix} a_1^{(1)} \\ . \\ . \\ a_m^{(1)} \\ \end{bmatrix} = \begin{bmatrix} x_1 \\ . \\ . \\ x_m \\ \end{bmatrix} \]となります。\( (x_1, x_2, ..., x_m) \)はこのネットワークへの外部からの入力信号です。 k番目の層のi番目のユニットからk+1番目の層のj番目のユニットへの信号に対する重みを\( w_{ji}^{(k)}\) と表記する。従って、入力層から隠れ層への信号に対する重み係数は行列形式となるので、これを \( W^{(1)} \) と表記します。同じように、隠れ層(第2層)から出力層への信号に対する重み係数は行列形式となるので、これを \( W^{(2)}\) と表記します。隠れ層における各ユニットでの入力信号の荷重和は
\[ z^{(2)} = W^{(1)} a^{(1)} + b^{(1)} \]という行列計算式となります。ここで、\( b^{(1)}\) は、入力層のバイアスユニットからの信号です。
第2層(隠れ層)の出力信号は活性化関数を用いて、
\[ a^{(2)} = \phi(z^{(2)}) \]と表現されます。多層ニューラルネットワークでは、各層について、同様な関係式が成立します。
\[ z^{(3)} = W^{(2)} a^{(2)} + b^{(2)} \\ a^{(3)} = \phi(z^{(3)}) \]ここで、\( b^{(k)}\) は、k番目の層のバイアスユニットからの信号です。
以下に、3層ニューラルネットワークの実装の例を示します。入力層ノードの出力数は2、第2層(隠れ層)のニューロン数は3、第3層(出力層)は2個となっています。第1層と第2層の活性化関数はsoftmax関数で、出力層での活性化関数はsigmoid関数です。ベクトル\( (b_1、b_2、b_3) \)はそれぞれ、第1、2、3層のバイアスユニットからの信号で、ニューロンからの出力信号と区別して表記してあります。入力層からの信号\( x \)は\( (1.0, 1.0) \) としてあります。
import numpy as np
def softmax(x):
exp_a = np.exp(x)
sum_exp_a = np.sum(exp_a)
y=exp_a/sum_exp_a
return y
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def init_network():
init_net = {}
init_net['W1']=np.array([[0.1,0.3,0.5],[0.2, 0.4, 0.6]])
init_net['W2']=np.array([[0.1, 0.4], [0.2, 0.5,], [0.3, 0.6]])
init_net['W3']=np.array([[0.1,0.3], [0.2, 0.4]])
init_net['b1']=np.array([0.1, 0.2, 0.3])
init_net['b2']=np.array([0.1, 0.2])
init_net['b3']=np.array([0.1, 0.2])
return init_net
def ppn(init_net, x):
w1, w2, w3 = init_net['W1'], init_net['W2'], init_net['W3']
b1, b2, b3 = init_net['b1'], init_net['b2'], init_net['b3']
z1 = np.dot(x, w1) + b1
a1 = sigmoid(z1)
z2 = np.dot(z1, w2) + b2
a2 = sigmoid(z2)
z3 = np.dot(z2, w3) + b3
y = softmax(z3)
return y
init_net = init_network()
x=np.array([1.0,1.0])
y=ppn(init_net, x)
print(y)
このコードを実行すると、[0.35939292 0.64060708]と結果が表示されます。この実装では、init_network() と ppn() という関数が定義されています。init_net = init_network() という命令で、重みとバイアスの初期値化を行い、その値を辞書型の変数 init_net に格納します。y=ppn(init_net,x) で入力信号xの値を渡して、ネットワークの出力を計算して、その値を渡します。この Google Colabからでも実行できます。
画像識別を行う深層学習では、こうした多層ニューラルネットワークの理論上の関係を前提にして、ネットワークの出力が正しい識別をするように、各層の重み係数\(w_1、w_2、w_3\)を学習することが課題となります。正しい識別の程度を測る判断基準として、識別誤差の関数を用います。推定の誤差の大きさを測る関数を損失関数と言います。代表的な損失関数は二乗和誤差で、以下のように定義されます。
\[ L(w) = \Sigma_k (y_k -z_k)^2 \]ここで、\( y_k\) はサンプルkの正解、\(z_k\) はサンプルkから予測された出力を表す。
損失関数を重き係数wの関数とする理由は推定すべきパラメータがwだからです。この損失関数を最小にするwの値が推定された(学習された)モデルのパラメータになります。重み係数の推定方法のうちで最も単純な手法は勾配降下法(Gradient Desccent method)と呼ばれるアルゴリズムです。勾配降下法(Gradient Desccent method)と誤差逆伝播法(backward propagation)の説明については、深層学習のページを参照ください。
一般的に機械学習では、訓練データとテストデータの2つに分けて、学習を行います。そして、テストデータを用いて学習を行い、その後で、そのパラメータを組み込んだモデルの有効性をテストデータを用いて評価します。この学習において、訓練データから指定した枚数(ミニバッチと言います)を選び出し、このミニバッチごとに学習を行います。例えば、1500枚のデータうち、100枚をランダムに選び学習を行います。これをミニバッチ学習と言います。通常は、このミニバッチ学習を何回も行います。1500/100=15回のミニバッチ学習を行うことをepoch1回の学習と言います。
二乗和誤差の他に損失関数として用いられる代表的な関数の一つは交差エントロピー誤差(cross entropy error)です。以下のように定義されます。
\[ L(w)= - \Sigma_k y_k \log z_k \]次に、多層パーセプトロン・モデルで学習を行うことを考えましょう。多層ニューラルネットワークを用いて、重み係数の推定学習で用いられる有名なデータセットとして、MNIST(Mixed National Institute of Standards and Technology)のデータセットが有名です。これは500人の手書き数字のデータを収集したものです。MNISTデータセットはY. LeCunのWebサイトで公開されています。MNISTデータセットは
トレーニングデータセットの画像:train-images-idx3-ubyte.gzの4種類から構成されています。LeCunのWebサイト で提供されている上記のファイルをダウンロードします。これらのファイルはダウンロードした後、gzipで解凍する必要があります。このデータセットをwotking directoryに配置して、
$ gzip *ubyte.gz -dとします。上記4つのファイルが解凍されます。
私のGitHubのリポジトリには、解凍された4つのファイルが保存されていますので、以下のようなPythonコードを実行するとデータが読み込まれます。
#mnist.py
import os
import struct
import numpy as np
def load_mnist(path, kind='train'):
"""Load MNIST data from `path`"""
labels_path = os.path.join('./',
'%s-labels-idx1-ubyte' % kind)
images_path = os.path.join('./',
'%s-images-idx3-ubyte' % kind)
with open(labels_path, 'rb') as lbpath:
magic, n = struct.unpack('>II',
lbpath.read(8))
labels = np.fromfile(lbpath,
dtype=np.uint8)
with open(images_path, 'rb') as imgpath:
magic, num, rows, cols = struct.unpack(">IIII",
imgpath.read(16))
images = np.fromfile(imgpath,
dtype=np.uint8).reshape(len(labels), 784)
return images, labels
以下に読み込まれたデータの一部を掲載します。

MNIST 手書き文字データ
以下の作業を行うにために必要なスクリプト類は私のGitHubから入手できます。
3層ニューラルネットワークの重み係数の推計アルゴリズムをPythonで実装したコードを見てみましょう。Jupyter Notebookを起動して、MNIST_MLP.ipynbを開いてください。このGoogle Colab上でも実行できます。推計と予測に使用されるクラス名は NeuralNetMLP モジュールです。出力層に使用される活性化関数はシグモイド関数が採用されています。その理由は、モデルの誤差の大きさを示す損失関数として対数尤度関数(log-likelihood)が使用されているからです。対数尤度関数を用いた誤差損失関数は
\[ J(w) = - \Sigma_{i=1}^{n} [ y_i \log (\phi(z_i^{(3)}) + (1- y_i) \log (1 - \phi(z_i^{(3)}) ] \]と定義されます。ここで、\( y_i \)はサンプルデータiの正しい数値、\( \phi(z_i^{(3)}) \) は活性化関数でシグモイド関数が採用されています。予測数値が正しい数値に近づくように、このロジステック回帰モデルで重み係数\( w \)の学習が行われます。このプログラムでの学習方法は、深層学習で定番の誤差逆伝播法(back propagation)が実装されています。詳しくは深層学習のページを参照ください。誤差逆伝播法の説明に関しては、深層学習の参考書、例えば、斎藤康毅著『ゼロから作るDeep Learning』(オライリー・ジャパン社)などの参考書を参照してください。
実際の作業を行なって見ましょう。MNIST_MLP.ipynbのセルを上から順番に実行してください。
MNISTデータセットは60000個のトレーニングサンプルと10000個のテストサンプルから構成され、数値データ(0,1,2,3,4,5,6,7,8,9)の手書き画像のシェイプは2次元(28, 28)なので、1次元のシェイプにして、28x28=784バイトのサイズにします。よって、入力層のユニット数は784となり、出力信号は10個のユニットからなります。nn = NeuralNetMLPクラスで、隠れ層のユニット数を50としてあります。epochs=800としてありますが、実行時間を気にしなければ、epochs=1000にしてもいいです。GPUを用いても学習に10分程度かかるでしょう。
入力文nn.fitの実行により、正しい重み係数を推定するための学習が開始されます。バイアスユニット分を加えて、第1層の重み係数行列、W1は50x785行列、第2層のそれはW2は10x51行列となっています。各サンプルデータには正解(labels, target values)が付属しているので、これとモデルの予測値が乖離する間は重み係数値の修正を繰り返します。修正方法には勾配降下法(gradient descen method)が使用されます。このプログラムでは1000×6万回の繰り返し計算が行われます(epochs=1000の時)が800×6万回程度で収束します。CPUの速度に依存しますが、時間は20分から30分程度かかります。テストデータにおける識別の正答率は95.62%となっています。4.38%はニューラルネットワークによる識別に誤りが発生しています。この正答率を改善するためには、層の深さをもっと大きくする必要があります。
類似のPythonコードは斎藤康毅著『ゼロから作るDeep Learning』のGitHub https://github.com/oreilly-japan/deep-learning-from-scratch に置かれているch05/train_neuralnet.pyです。第1層と隠れ層の間にsigmoid関数が挟まれているのはRaschka氏のプログラムと同じですが、相違する部分は、出力層の活性化関数としてsoftmax関数が採用されているところと、損失関数には交差エントロピー(cross entropy)が使用されている部分です。この交差エントロピー誤差を使用するときには、データ入力でone-hot-label=trueと設定する必要があります。
いずれにしても、ニューラルネットワークの理論では、調整可能な重み係数が想定され、この重み係数をサンプルデータにフィットするように調整することを学習と呼んでいる。勾配降下法を用いた学習過程は以下の3ステップから構成されます。
(1)サンプルデータの中からランダムに一定数のデータを取り出す。を損失関数が最小値の近傍に達するまで繰り返す。
簡単に言えば、、ニューラルネットワークにおける学習は損失関数の最小値を実現するパラメータの値を推定することです。これは最適なパラメータ(重み係数)を見出す問題で、最適化問題の一つです。ニューラルネットワークの層が深くなるにつれて、パラメータは極めて多数にのぼり、複雑になるので、その最適化は難しい問題です。この最適化問題を解くアルゴリズムとして、様々な手法が提案されています。SGD(stochastic Gradient descent)やAdaGradと呼ばる手法がありますが、その説明は、斎藤康毅著『ゼロから作るDeep Learning』などの参考書を参照ください。
PythonライブラリのScikit-learnを活用すれば、多層パーセプトロンモデルを簡単な入力作業で便利に利用できます。scikit-Learnを使った簡単な機械学習
をみてください。
畳み込みニューラルネットワーク(CNN)とは何か |
deep learningはロボット操作、自動運転、遠隔医療技術、音声探索・案内など様々な分野に実用化され、活用されている。これらの応用技術の元になっている理論はCNN(Covolutional Neural Networks) と言われる枠組みの上で発展してきたものです。上記の実用技術における具体的な実装プログラムを説明することは私の能力を大きく超えます。とはいえ、「そうなっています」で終わりにするわけにもいかないので、CNNの大まかな説明は必要かもしれません。ここで、CNNの大まかな紹介をしてみます。
パーセプトロン概念を用いた多層パーセプトロンのニューラルネットワークでは、隣接する層のすべてのニューロンが互いに結合していました。これを全結合と呼び、denseなネットワーク(fully connected)となっています。このdenseなニューラルネットワークでは、層と層の間に活性化関数が入っていても、各層のニューロンは前の層のすべてのニューロンからの信号を受け取ります。
これに対して、CNNはその名前の通り、全結合層が多層化されるのではなく、convolution layer層とpooling layer層(subsampling層ともいう)という新しい層が加わります。言い換えれば、convolution層とpooling層が交互に配置され、最終部分に全結合層が配置される多層ニューラルネットワークです。CNNでは、入力情報の空間的な情報が無視されてしまうという情報の損失を回避することができます。上記のMNISTデータ分類のモデルを見れば明らかな通り、入力画像の形状は3次元(1,28,28)ですが、全結合層に入力する場合、28x28の1次元情報に変換しました。畳み込み層は入力画像の形状を維持します。入力データが画像である場合、画像の3次元データを3次元データとして次の層に移します。CNNでは、畳み込み層の入出力データを特徴マップ(feature map)といい、入力データを入力特徴マップ、出力データを出力特徴マップと言います。
ここで、畳込みについて説明します。畳み込みの計算は少々分かり難いです。畳み込みのカーネル(フィルター)行列Kが3✕3行列のケースが下に描かれています。
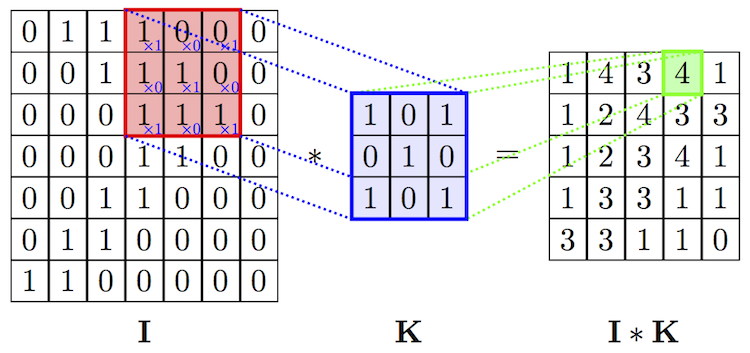
カーネルの枠を一定間隔で入力データIの行列枠上をスライドさせます。各スライドごとに、カーネル行列の要素と入力データの対応する要素をそれぞれ乗算し、その総和をもとめて、この総和値を特徴マップ(feature maps)に移します。上の例では1x1+0x0+1x0+0x1+1x1+0x0+1x1+0x1+1x1=4と計算されています。
max poolingとはフィルター行列で覆われた行列中の最大値をその行列の代表値にすることです。2x2フィルターによるmax poolingでは、入力データを2✕2行列ごとに覆い、2✕2行列の中の最大値を取り、その値を出力信号として送ります。この結果データサイズが縮小されます。下の図を見るとよく分かります。
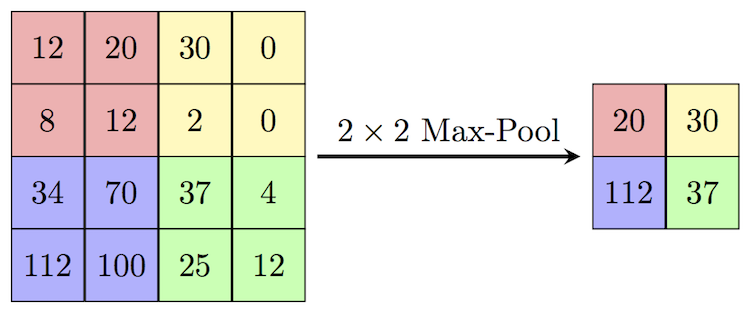
代表的なCNNでは、交互に並べられた畳込み層とプーリング層の後に、Classificationと呼ばれる多層パーセプトロンが配置されます。多層パーセプトロンは基本的にはすべてのユニットが結合されている構造を持つので、fully connected layersという言葉が使われています。畳込み層とプーリング層を重ねることによって入力データの各特徴がより明確に抽象化されます。こうして抽象化された各特徴を手がかりとして、最後の多層パーセプトロンの部分が入力データの分類を実行します。このことから、多層パーセプトロンの部分は分類器とも呼ばれる機能を持ちます。
CNNの基本構造を易しく分かりやすく説明することを試みました。少しは理解が深まったことと信じます。