
|
Pythonの機械学習用のライブラリであるScikit-learnを取り上げて、実際の課題に挑戦します。scikit-learnライブラリの使用をするにあたっては、パーセプトロン・モデルに学習させる課題を取り上げることが便利である。scikit-learnにはirisデータセットや手書き数字のデータなど便利なデータベースが含まれているいます。
Scikit-learn は Pythonで書かれているので、Pythonの基礎的な知識を持っている人を想定します。Python 入門の説明はPython Tutorials のページを参照ください。 scikit-learnの公式ホームページはhttp://scikit-learn.org/stable/index.htmlです。このサイトには使用方法の詳しいドキュメントが掲載されています。
Googleが提供するGoogle Colaboratoryは、Jupyter Notebook をベースとした、Googleの仮想マシン上で動くPython実行環境です。Googleアカウントを登録すれば、インストール等の作業に手間を取られることなく、すぐに機械学習のコードを実行することができます。AIや機械学習に関するページで説明されるPython コードを自分の手で実行したいと希望する方は、Googleのアカウント登録、および、GitHubのアカウントの登録をすることをお勧めします。両方とも無料で行えます。
Last updated: 2022.2.20(2018年4月22日開設)
Scikit-learnの基本的使用方法:iris dataを用いた機械学習 |
最初に、主要なディープラーニング用のパッケージをインストールします。
$ python3 -m pip install numpy scipy pillow pydot matplotlib seaborn scikit-learn scikit-image keras pandas opencv-python
以下のモジュール・パッケージを使用しました。
numpy 1.20バージョンは最新のものにアップデートしてください。旧バージョンのscikit-learnがインストールされている場合、以下のようなコマンドを入力してアップデートします。
$ pip install -U scikit-learn
scikit-learnの機能はsklearnという名称のライブラリに組み込まれます。sklearnの中身を見てみると、以下のようになっています。
MacBook-Air:sklearn koichi$ ls __check_build kernel_approximation.py __init__.py kernel_ridge.py __pycache__ learning_curve.py _build_utils linear_model _isotonic.cpython-36m-darwin.so manifold base.py metrics calibration.py mixture cluster model_selection covariance multiclass.py cross_decomposition multioutput.py cross_validation.py naive_bayes.py datasets neighbors decomposition neural_network discriminant_analysis.py pipeline.py dummy.py preprocessing ensemble random_projection.py exceptions.py semi_supervised externals setup.py feature_extraction svm feature_selection tests gaussian_process tree grid_search.py utils isotonic.py
この中で、datasetsというモジュールには、機械学習で必須のアヤメの標本データ及び手書き数字のデータが収められています。実際に、これらのデータを読み込んで見ましょう。loads.digitsは手書き数字のデータ、loads.irisはアヤメのデータを読み込みます。jupyter notebook を起動した後、新規にノートブックを作成して、以下のコードを最初のセルにコピペしてください。
from sklearn import datasets iris = datasets.load_iris() x = iris.data y = iris.target print(x)
このセルを「Run」をクリックして実行します。iris.dataの中身が以下のように表示されます。アヤメのデータセットを見て見ましょう。アヤメのデータセットには150枚のアヤメの計測データが収録されています。特徴量は4種類で、がくの長さと幅の大きさ、花びらの長さ、幅の大きさ、となっています。
[[ 5.1 3.5 1.4 0.2] [ 4.9 3. 1.4 0.2] [ 4.7 3.2 1.3 0.2] [ 4.6 3.1 1.5 0.2] [ 5. 3.6 1.4 0.2] --- [ 6.7 3. 5.2 2.3] [ 6.3 2.5 5. 1.9] [ 6.5 3. 5.2 2. ] [ 6.2 3.4 5.4 2.3] [ 5.9 3. 5.1 1.8]]
のように4つのデータの配列になっています。iris.targetには各計測データに対応するアヤメの種類が収納されています。アヤメの種類はsetosa、 versicolor、 virginicaの3つに分類されます。「+」をクリックして、セルを追加して、そこに以下のコードをコピペします
import numpy as np
print("Class labels:", np.unique(y))
このセルを実行すると
labels: [0 1 2]
となっていることがわかります。アヤメの種類setosa、 versicolor、 virginicaを分類番号 [0, 1, 2] にクラス分けしています。unique(y)は異なる数字のみからなる配列に変換することです。アヤメの花びらについて知らない読者もいると思われますので、下にアヤメの写真を掲載します。

次に、手書き数字のデータセットを見て見ましょう。以下のコードを新しいセルにコピペして実行します。
digits = datasets.load_digits() print(digits.data)
[[ 0. 0. 5. ..., 0. 0. 0.] [ 0. 0. 0. ..., 10. 0. 0.] [ 0. 0. 0. ..., 16. 9. 0.] ..., [ 0. 0. 1. ..., 6. 0. 0.] [ 0. 0. 2. ..., 12. 0. 0.] [ 0. 0. 10. ..., 12. 1. 0.]]
となっています。以下のコードを新しいセルにコピペして、実行します。
x=digits.data y=digits.target print(x.shape) print(y.shape) ---- (1797, 64) (1797,)
となります。データの個数は1797個です。手書き数字の特徴データは8x8=64ピクセルの特徴量から構成されています。ターゲットは手書き数字の正解なので、データの個数と同じです。

MNIST 手書き文字データ
実は、機械学習で一般的に利用されているMNISTデータセットはscikit-learnに付属しているデータに比較して巨大な大きさです。画像のピクセル数は28x28=784であり、学習用画像が6万枚、テスト用画像が1万枚となっています。研究論文を書くために使用する訳ではないので、ここでは、scikit-learnに付属のデータセットを用います。MNISTデータセットの使用については、このページを参照してください。
次に、scikit-learnを用いて、パーセプトロン・モデルの重み係数の学習(トレーニング)をさせてみましょう。Jupyter Notebookを起動して、以下のコードをセルにコピペしてください。このGoogle Colabで、セルの左上の三角形をクリックすれば実行できます。学習に特徴量の第3、4列 data[:, [2, 3]](花びらの長さと幅の大きさ)を使います。
from sklearn import datasets
import numpy as np
from sklearn.linear_model import Perceptron
iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target
print('Class labels:', np.unique(y))
ppn = Perceptron(max_iter=10000, tol=0.00001, random_state=1)
#ppn = Perceptron(n_iter=400, eta0=0.00001, random_state=0)
ppn.fit(X,y)
y_pred = ppn.predict(X)
print('Misclassified samples: %d' % (y != y_pred).sum())
from sklearn.metrics import accuracy_score
print('Accuracy: %.2f' % accuracy_score(y, y_pred)
from sklearn.linear_model import Perceptron
でパーセプトロンモデルを読み込んでいます。トレーニングの繰り返し回数を最大で10000回として、損失関数値の減少が0.00001以下になると終了します。random_state=1 は、学習ごとにランダムに選択したデータセットを用いることを指定します。(y != y_pred).sum() は、予測された結果(y_pred)が正解ラベル(y)と異なるケースの回数の和を取ることを意味します。accuracy_score(y, y_pred) は、予測の正解率を計算します。このトレーニングの結果を用いて、計測データに適用した時の予測の誤答の数と正解率は
Misclassified samples: 50
Accuracy: 0.67
となります。
次に、データセットをトレーニングデータとテストデータセットに分割して、ミニバッチ様式で学習させて見ましょう。
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0)
データ全体のうち、30%をテストデータ、残り70%をトレーニングデータとします。機械学習の最適化アルゴリズムで、性能の高い結果を得るための手法として、特徴量の標準化(スケーリング)を行います。クラスStandardScaler()が特徴量の標準化を実行するためのインスタンスです。インスタンス名を sc とします。
from sklearn.preprocessing import StandardScaler sc = StandardScaler() sc.fit(X_train) X_train_std = sc.transform(X_train) X_test_std = sc.transform(X_test)
sc.fit(X_train)で平均値と標準偏差を計算します。sc.transform(X_train) はX_train の値を(X_train - 平均値)/ 標準偏差に変換します。
次に、標準化したデータを用いて、パーセプトロンモデルをトレーニングします。
from sklearn.linear_model import Perceptron
ppn = Perceptron(max_iter=40, tol=0.1, random_state=0)
ppn.fit(X_train_std, y_train)
y_pred = ppn.predict(X_test_std)
print('Misclassified samples: %d' % (y_test != y_pred).sum())
from sklearn.metrics import accuracy_score
print('Accuracy: %.2f' % accuracy_score(y_test, y_pred))
となります。y_test は45個のサンプルなので、そのうち15個に対して間違った予測をしたことになります。正解率は67%となります。
パーセプトロンモデルの学習から得られた予測の決定境界をプロットし、データサンプルをどの程度分類に成功しているかどうかを可視化して見るためために、以下のplot_decision_regions 関数を使用する。ここで使用するコードの多くは、Sebastian Raschka氏による”python-machine-learning-book/code/ch03/"にあるサンプルコードを若干修正したものです。このGoogle Colabで、plot_decision_regions関数の定義というタイトル以下のセルの左上の三角形を順次クリックすれば実行できます
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
# setup marker generator and color map
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# plot the decision surface
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0],
y=X[y == cl, 1],
alpha=0.6,
c=cmap(idx),
edgecolor='black',
marker=markers[idx],
label=cl)
# highlight test samples
if test_idx:
# plot all samples
X_test, y_test = X[test_idx, :], y[test_idx]
plt.scatter(X_test[:, 0],
X_test[:, 1],
c='',
alpha=1.0,
edgecolor='black',
linewidths=1,
marker='o',
s=55, label='test set')
このコードの後に、
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))
plot_decision_regions(X=X_combined_std, y=y_combined,
classifier=ppn, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
# plt.savefig('./figures/iris_perceptron_scikit.png', dpi=300)
plt.show()
を実行すると、以下のグラフが得られます。
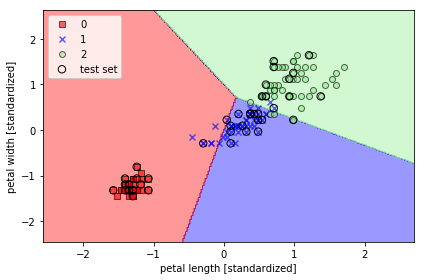
このグラフからわかる通り、3つの品種を線形の境界で完全に分離することはでなきい。これがパーセプトロンモデルの限界です。
ここで、パーセプトロンモデルを用いたロジスティック回帰分析の説明します。モデルの構造は以下のようになっています。
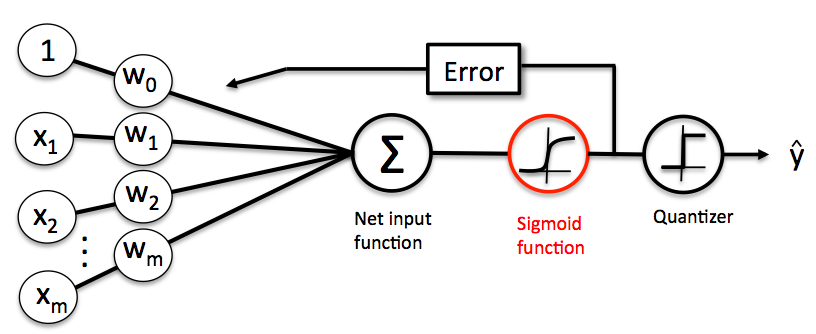
入力信号の荷重和の値がロジスティック曲線にインプットされて、その出力値に対して勾配降下法による重み係数\( w \)の学習が行われます。そのとき採用される損失関数は対数尤度関数にマイナスをかけたものです。重み係数の学習については、Deep Learningの基礎を参照ください。
scikit-learn には非常に最適化されたロジスティック回帰のコードが実装されていて、多種クラスの分類が標準でサポートされています。ここでは、上で使用したデータセットを用いて、scikit-learn に組み込まれたモジュールを利用したロジスティック回帰分析をして見ます。
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(C=1000.0, random_state=0)
lr.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined,
classifier=lr, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
from sklearn.linear_model import LogisticRegression でロジスティック回帰分析のモジュールを読み込んでます。Cは正則化パラメータの逆数です。Cの値を大きくすることは、正則化の強さを弱める役割をします。ロジスティック回帰の正則化された損失関数は
\[
J(w) = C \sum _{i=1}^n [ -y^{(i)} \log (\phi(z^{(i)}) - (1 - y^{(i)} ) \log (1 - \phi(z^{(i)})) ] + \frac{1}{2} \|w \| ^2
\]
と与えられる。ここで、\( y^{(i)} \) は教師ラベル、\( z^{(i)} \) は入力の荷重和です。\( \phi \) はsigmoid 関数(ロジスティック曲線)です。
過学習を防ぐための正則化についての理論は、機械学習の理論的な専門書を呼んでください。
サポートベクトルマシン(SVM)を用いた機械学習 |
ここで、サポートベクトルマシン(support vector machine: SVM)を用いたアヤメの分類学習を取り上げます。SVM は広範に利用されている学習アルゴリズムで、パーセプトロンモデルの拡張とも言えます。SVMでの学習は、各品種を分類する境界(超平面)と、この超平面に最も近いトレーニングデータとの距離を最大化することを目指します。超平面に最も近いトレーニングデータとの距離をマージンと言います。超平面に最も近いトレーニングデータのサンプルをサポートベクトルと呼びます。
SVM はパーセプトロンモデルと同じ限界を持っているにも関わらず、人気が高いのはなぜでしょうか。非線形の問題に対して、「カーネル化」することが容易であることに理由があります。とりあえず、SVMによる境界(超平面)確定問題の実際を見て見ましょう。以下のコードを見てください。
from sklearn.svm import SVC
# 分類用にサポートベクトルマシンを用意
svm = SVC(C=1.0, kernel='linear', random_state=0)
svm.fit(X_train_std, y_train)
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))
plot_decision_regions(X=X_combined_std, y=y_combined,
classifier=svm, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()
このコードを見てすぐに理解できるように、パーセプトロンモデルのトレーニングと異なる箇所は、ppn が svm に入れ替わったところだけです。from sklearn.svm import SVC で、サポートベクトルマシンによる分類器(support vector machine for classification: SVC)を読み込んでいます。kernel='linear' は線形サポートベクトルマシンを組み込むためのオプションです。C=1.0 はマージンを計算するときの関数のパラメータの値をデフォルト値に指定することです。このコードを実行すると、SVMの決定境界が図示されます。しかし、パーセプトロンモデルと同じく、3つの品種をこの境界で完全に分離することはできません。Google Colab の「1.2 線形サポートベクトルマシンの採用」以下のセルで実行できます。
ここで、カーネルトリックという操作が必要となります。カーネルトリックとは、分類の境界となる超平面を直線や平面ではなく、曲線や曲面にしてしまおうとする操作のことです。データ2点間の関係を表現する関数をカーネルと言います。このカーネル関数を用いてマージンを最大化するトレーニングが行われます。カーネル関数を2点間の距離のみの関数と想定するとき、動径基底関数(radial basis function)と言います。sklearnで採用されている動径基底関数はガウスカーネルと呼ばれる以下の関数です。二つのデータを\( x^{(i)}, x^{(j)} \)と表記するとき、
\[ k(x^{(i)}, x^{(j)}) = \exp (-\gamma \|x^{(i)} - x^{(j)} \|^2) \] と表現される関数をRBFカーネルと言います。ここで、\( \gamma \)は \[ \gamma = \frac{1}{2\sigma} \]で表現されるハイパーパラメータです。カーネルと呼ばれる理由は、二つのサンプル間の類似性を表現すると解釈されるからです。類似度は同一のサンプルのときに1となり、全く類似性がないときには0となります。\( \gamma \)の値が大きくなるほど、曲線の曲がり方が急進になります。\( \gamma = 0.1 \)がカットオフ値になります。このカーネル関数を利用するときは、例えば、
svm = SVC(kernel='rbf', gamma=0.5, random_state=0, C=1.0)と書きます。境界の曲線の曲がりをより強くしたいときは、
svm = SVC(kernel='rbf', gamma=1.0, random_state=0, C=1.0)のように、\( \gamma \)の値を大きくします。
from sklearn import datasets
import numpy as np
iris = datasets.load_iris()
X = iris.data[:, :2]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0)
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
from sklearn.svm import SVC
svm = SVC(kernel='rbf', gamma=0.5, random_state=0, C=1.0)
svm.fit(X_train_std, y_train)
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))
plot_decision_regions(X=X_combined_std, y=y_combined,
classifier=svm, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()
このコードでは、特徴量をX = iris.data[:, :2](sepal length, sepal width)に変更してみました。結果は以下の通りです。
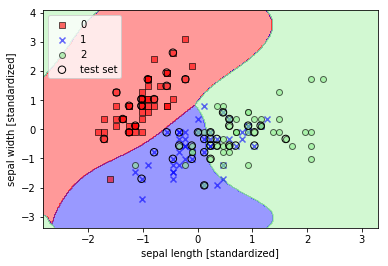
4つの特徴量全てを用いて、アヤメ3品種の分類を行います。以下のコードを見てください。
iris = datasets.load_iris()
# 4つの特徴量のセットを変数Xに、ターゲット(教師ラベル)を変数yに格納
X = iris.data
y = iris.target
svm = SVC(C=1.0, kernel='linear', random_state=0)
svm.fit(X, y)
result = svm.predict(X)
print('ターゲット(教師ラベル)')
print(y)
print('機械学習による予測')
print(result)
total = len(X)
success = sum(result==y)
print('正解率:%表示')
print(100.0*success/total)
このコードを実行すると、以下の結果が得られます。
ターゲット(教師ラベル) [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2] 機械学習による予測 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2] 正解率:%表示 99.33333333333333
誤分類は1箇所だけですが、正解率を100%にする完全な識別は不可能です。現実のデータでは、超平面で100%の正解率で分類できることはあり得ません。言い換えると、線形の超平面で分離可能なデータは現実には殆どありません。
多層パーセプトロンモデルを用いた機械学習 |
次に、多層パーセプトロンモデルを使った学習問題を取り上げます。以下が3層ニューラルネットワークを使用したトレーニング用のコードです。コードは、このGoogle Colabにあります。
from sklearn import datasets
import numpy as np
from sklearn.neural_network import MLPClassifier
iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target
mlp = MLPClassifier(hidden_layer_sizes=(100, ), max_iter=10000, tol=0.0001, random_state=1)
#mlp = MLPClassifier(hidden_layer_sizes=(100, ), max_iter=10000, tol=0.00001, random_state=None)
mlp.fit(X, y)
y_pred = mlp.predict(X)
from sklearn.metrics import accuracy_score
print('Class labels:', np.unique(y))
print('Misclassified samples: %d' % (y != y_pred).sum())
print('Accuracy: %.2f' % accuracy_score(y, y_pred))
このトレーニングから得られるモデルの予測をデータに適用した時の予測の正解率は
Misclassified samples: 7
Accuracy: 0.95
となり、単純パーセプトロンモデルに比較して、予測の精度が改善されます。
4種類の特徴を用いて分類を行うと、より予測の精度は改善されます。上のスクリプトで、X = iris.data[:, [2, 3]] をX = iris.data と修正して、コードを実行してください。正解率は0.99に上昇します。線形サポートベクトルマシンでは誤識別は1回、正解率は99.3%でしたから、分類器としての性能は優れているとは言えません。とは言え、学習の時間を長くすれば、正解率は100%に近づきます。その分、時間はかかります。
主成分分析(Principal Component Analysis)による次元圧縮 |
主成分分析(Principal Component Analysis: PCA)は様々な分野において使用されている線形変換法で、データ情報の次元削減のためによく利用されています。PCAは、特徴量同士の相関関係に基づいてデータからパターンを抽出するのに役に立つます。高次元データにおいて分散が最大となる方向を見つけ出して、元の次元よりも低い次元の部分空間へ射影する手法です。この新しく作成された部分空間では、分散が最大となる方向に座標系の軸を設定します。
元のデータの次元が\( d \)であるとします。サンプルデータを
\[ x= (x_1, x_2, ..., x_d) \in R^d \]と表記します。PCAで次元を\( k \)に削減するとして、そのための変換行列を\( W \)とすると、\( W \)は\(d \)行\( k \)列の行列となります。
\[ W \in R^{d \times k} \]したがって、
\[ z = x W =(z_1, z_2, ..., z_k) \in R^k \]とすると、元の\( d \)次元データは\( k (\ll d) \)次元の部分空間の要素\( z \)に変換されます。
次元削減のためのPCAのアルゴリズムは以下のようなステップから構成されます。
pythonのNumpyモジュールに組み込まれたlinalg.eig 関数を使えば簡単に固有値と固有ベクトルを計算できます。なので、Numpyモジュールを利用すればPCAはpythonで実装できます。しかし、ここではより簡易な方法を利用します。つまり、Scikit-learnにこのアルゴリズムを組み込んだPCAクラスを活用します。このPCAクラスを用いてロジスティック回帰分析を行ってみましょう。
PCAクラスの使用に関する詳細な説明は、Scikit-Learnのweb サイト内のこのドキュメントを見てください。
元になるデータセットを用意します。ここでは、pandaライブラリを使用して、UCI Machine Learning Repository からワインのデータセットを読み込みます。以下のスクリプトを実行してください。このコードは、Google Colabで実行できます。
import pandas as pd
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/'
'machine-learning-databases/wine/wine.data',
header=None)
df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash',
'Alcalinity of ash', 'Magnesium', 'Total phenols',
'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins',
'Color intensity', 'Hue',
'OD280/OD315 of diluted wines', 'Proline']
df_wine.head()
ワインのデータセットが読み込まれたことを確認できます。
0 1 14.23 1.71 2.43 15.6 127 2.80 3.06 0.28 2.29 5.64 1.04 3.92 1065 1 1 13.20 1.78 2.14 11.2 100 2.65 2.76 0.26 1.28 4.38 1.05 3.40 1050 2 1 13.16 2.36 2.67 18.6 101 2.80 3.24 0.30 2.81 5.68 1.03 3.17 1185 3 1 14.37 1.95 2.50 16.8 113 3.85 3.49 0.24 2.18 7.80 0.86 3.45 1480 4 1 13.24 2.59 2.87 21.0 118 2.80 2.69 0.39 1.82 4.32 1.04 2.93 735
このデータセットは、178個のワインサンプルとそれらの化学的性質を示す13の特徴量で構成されている。 第1列目はサンプル番号です。2列目がワインのクラス分類です。ワインのクラスは3種類で、そのラベルは[1, 2, 3]となっています。3列目はアルコール度数です。
慣例通り、データセットをトレーニングデータとテストデータに分割して、標準化を行います。df_wine.iloc[:, 0].values は、配列 index 0 のデータ、つまり、ワインのクラスラベルの値をy に格納します。df_wine.iloc[:, 1:].values はindex 1 以降、13種の特徴量のデータ配列を格納します。
from sklearn.model_selection import train_test_split
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test = \
train_test_split(X, y, test_size=0.3, random_state=0)
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)
次に、"from sklearn.decomposition import PCA" と入力して、クラスPCAを使用可能になるように読み込みます。pca = decomposition.PCA(n_components=2)でPCAを実施したときに主成分軸の数を2本に設定します。PCAには以下のメソッドがあります。
fit(X[, y]) Fit the model from data in X.このメソッドのうち、X_transformed = pca.fit_transform(X)で、元のデータからモデルをフィットさせ、2次元のデータに変換します。以下のスクリプトを見てください。
import numpy as np from sklearn.decomposition import PCA pca = PCA(n_components=2) X_train_pca = pca.fit_transform(X_train_std) X_test_pca = pca.transform(X_test_std)
print("主成分(PC1、PC2)の分散説明率")
print(pca.explained_variance_ratio_)
print("固有ベクトル")
print(pca.components_)
主成分(PC1、PC2)の分散説明率 [0.37329648 0.18818926] 固有ベクトル [[ 0.14669811 -0.24224554 -0.02993442 -0.25519002 0.12079772 0.38934455 0.42326486 -0.30634956 0.30572219 -0.09869191 0.30032535 0.36821154 0.29259713] [-0.50417079 -0.24216889 -0.28698484 0.06468718 -0.22995385 -0.09363991 -0.01088622 -0.01870216 -0.03040352 -0.54527081 0.27924322 0.174365 -0.36315461]]
二つの主成分(PC1、PC2)の分散説明率を合計すると、0.56となっています。これは、2つの主成分がデータ情報の56%を説明することを意味します。 特徴の部分空間の散布図を描くために、前節で用いたプロット関数plot_decision_regions を定義します。
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
def plot_decision_regions(X, y, classifier, resolution=0.02):
# setup marker generator and color map
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# plot the decision surface
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# plot class samples
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0],
y=X[y == cl, 1],
alpha=0.6,
c=cmap(idx),
edgecolor='black',
marker=markers[idx],
label=cl)
そして、以下のコードを実行します。
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr = lr.fit(X_train_pca, y_train)
plot_decision_regions(X_train_pca, y_train, classifier=lr)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()
この結果は下のグラフのように描かれます。ここで用いた分類器はロジスティック回帰モデルです。
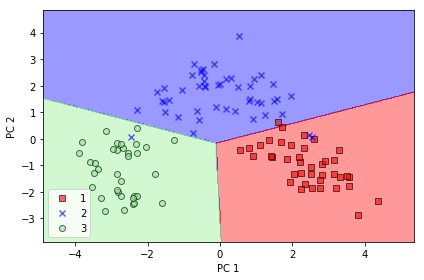
テストデータの分類の散布図を描くときは、上記のスクリプトで、plot_decision_regions(X_test_pca, y_test, classifier=lr) と修正します。
MNIST data-setを用いた機械学習 |
次に、機械学習で一般的に利用されているMNISTデータセットにPCAを応用して見ましょう。手書き数字のデータセットを見て見ましょう。以下のコードを入力すると、サンプルのサイズがわかります。
digits = datasets.load_digits() x=digits.data y=digits.traget print(x.shape) print(y.shape)
数値の画像データは8x8=64、データサンプル数は1797個です。
MNISTデータをPCAを用いて3次元データに変換し、それを散布図に描くコードが下のスクリプトです。(このサンプルコードは、金丸隆志『RaspberryPiで始める機械学習』BLUEBACKSから援用したものです。)このコードは、このGoogle Colabの「2.1 MNISTデータセットの手書き数字の分類:MNIST data-set with SVM」以降のセルにあります。
from sklearn import decomposition
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
pca = decomposition.PCA(n_components=3)
X_pca = pca.fit_transform(X)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel('PC1')
ax.set_ylabel('PC2')
ax.set_zlabel('PC3')
def getcolor(cl):
if cl==0:
return 'red'
elif cl==1:
return 'green'
elif cl==2:
return 'blue'
elif cl==3:
return 'cyan'
elif cl==4:
return 'magenta'
elif cl==5:
return 'yellow'
elif cl==6:
return 'black'
elif cl==7:
return 'orange'
elif cl==8:
return 'purple'
else:
return 'gray'
colors = list(map(getcolor, y))
ax.scatter(X_pca[:,0], X_pca[:,1], X_pca[:,2], color=colors)
plt.show()
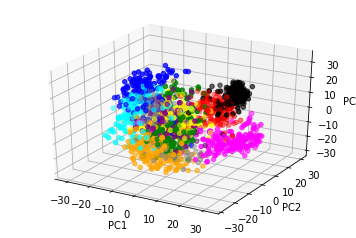
MNISTデータセットを用いた機械学習を取り上げます。MNISTデータセットを読み込んで、分類器にかけるコードは以下のようになります。サポートベクトルマシンを分類器として使っています。
from sklearn import datasets, svm
digits = datasets.load_digits()
X = digits.data
y = digits.target
svm = svm.SVC(C=1.0, kernel='linear', random_state=0)
svm.fit(X, y)
y_pred = svm.predict(X)
acc = sum(y_pred==y)/len(X)
print('training accuracy = % .2f%%' % (acc * 100))
このコードを実行すると、正解率は100%となります。このケースは、学習に用いたトレーニングデータそのものを使って正解率を求めているので当然でしょう。トレーニングデータとテストデータに分けて、トレーニングデータで学習させた結果を用いて、テストデータでの正解率を予測するとどうなるでしょうか。おそらく、正解率100%が実現できないと予想されます。以下のコードを見てください。元のデータセットの30%をテストデータにしています。
from sklearn import datasets, svm
digits = datasets.load_digits()
X = digits.data
y = digits.target
#from sklearn.cross_validation import train_test_split
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0)
from sklearn.svm import SVC
svm = SVC(C=1.0, kernel='linear', random_state=0)
svm.fit(X_train, y_train)
y_test_pred = svm.predict(X_test)
acc = sum(y_test_pred==y_test)/len(X_test)
print('Test data accuracy = % .2f%%' % (acc * 100))
このコードを実行すると、
Test data accuracy = 97.41%となります。当然ながら、正解率は100%に届きませんが、相当に高い正解率です。正解率が100%に届かない要因の一つは、画像のピクセル数が8x8=64という少なさにあります。以下のコードを実行すると、画像の内容が見えます。
import matplotlib.pyplot as plt
fig, ax = plt.subplots(nrows=2, ncols=5, sharex=True, sharey=True,)
ax = ax.flatten()
for i in range(10):
img = X_train[y_train == i][0].reshape(8, 8)
ax[i].imshow(img, cmap='Greys', interpolation='nearest')
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.show()
from sklearn import datasets, svm
import numpy as np
from sklearn.linear_model import Perceptron
digits = datasets.load_digits()
X = digits.data
y = digits.target
ppn = Perceptron(max_iter=10000, tol=0.00001, random_state=0)
ppn.fit(X,y)
y_pred = ppn.predict(X)
acc = sum(y_pred==y)/len(X)
print('training accuracy = % .2f%%' % (acc * 100))
from sklearn import datasets
import numpy as np
from sklearn.neural_network import MLPClassifier
digits = datasets.load_digits()
X = digits.data
y = digits.target
mlp = MLPClassifier(hidden_layer_sizes=(100, ), max_iter=50000, tol=0.00001, random_state=1)
#mlp = MLPClassifier(hidden_layer_sizes=(100, ), max_iter=10000, tol=0.00001, random_state=None)
mlp.fit(X, y)
y_pred = mlp.predict(X)
from sklearn.metrics import accuracy_score
#print('Class labels:', np.unique(y))
print('Misclassified samples: %d' % (y != y_pred).sum())
print('Accuracy: %.2f' % accuracy_score(y, y_pred))