|
自然言語データや時系列データは入力変数の中に系列依存関係の複雑さをもつので、このような系列依存データを用いた推論や予測問題は機械学習問題の中でも困難なもので、画像識別や物体検出問題よりも一段と複雑な課題になります。
時系列データの代表例として想定できるものは、電波、音声波形、株価指数、為替レート、気温変化などです。通念では時系列データとして想定されないものとして、文章(単語列)などがあります。電波の波形なら一定の時間間隔でのサンプル値になりますし、文章なら単語を前から並べたときの番号になります。文章生成ならば、今までの単語列を入力として、もっともらしい次の単語を予測することが課題となります。正しい文章(the monkey ate the apple)を繰り返しLSTMに覚えさせる(重みベクトルを更新する)ことで、"monkey"の後に"ate"が来るようなルールを学習することができます。音素・音声認識の場合、今までの音声波形(orその特徴量)を入力として、その時点で発話されている音素を予測することが課題になります。
系列連鎖を持つデータの予測においては、各入力信号が独立した入力ではなく、ある種の関係性をもつ一連の入力データとして取り扱い、これらの入力信号に対応した一連の出力データとして出力することが必要となります。単純なニューラルネットワークでは、出力は最後の層からのみ発生するため、一連の入力に対して一連の出力を生成することはできません。部分的ネットワークの出力を別のネットワークの入力として利用するような再帰的構造を持ったモデルは Recurisive Neural Network と呼ばれます。このネットワークモデルでは、ある層の出力は、次の層の入力として利用されるだけでなく、その後の複数の層の入力データとしても利用されます。RNN の拡張版は LSTM と呼ばれます。
このページでは、Keras及びPytorchのライブラリを用いて、 RNN 及び LSTM ネットワークをどのように実装できるかを説明します。最初の例として経済データの時系列を取り上げますが、他の時系列データ、例えば、気温変動のデータや旅客数データなどにも応用可能です。
Last updated: 2020.4.22(first uploaded 2019.4.26)
株価指数の予測問題 |
ファイナンス理論はブラック=ショールズ方程式を基礎としているが、この確率微分方程式は株価がランダムに変動する(幾何ブラウン運動)という前提で成り立っている。正確に株価の変動を予測することはほぼ不可能に近い。株価の急激な変動は、株式市場の外での経済的政治的要因に多くを依存しており、人々のデマやカオス的感情に作用されてもいる。
deep learningの手法を活用すれば、翌日の日経平均終値騰落予測はある程度の確率で予測できる。予測に必要な過去の株価データはネット上に公開されており、誰でも容易に入手できる。株価の時系列データは高々数千件程度しかないため、学習もすぐ終わるので、パラメーターをいろいろ変えてその影響を見るということは、容易にできる。 こうして、株価予測というテーマは、誰にでも簡単にできて、deep learningを利用した時系列予測問題に有益なテーマと言える。
とはいえ、このページで行う予測は、あくまでも、練習問題であって、現実で株投資のために使用するためのものではありません。株での資金運用はファイナンス理論が教える通り、的確なポートフォリオを組んで行ってください。
株価のデータはyahoo finaceあるいは日経平均株価(N225)からダウンロードします。
[Time Period]欄で「Max」などを指定して[Apply]し、[Download Data]リンクをクリックすればダウンロードできます。
ダウンロードしたファイルをExcelなどの表計算ソフトで開いてみると、取引の無い日付の行にnullが入っているので、そのような行を削除します。次に、株価データ(取りあえず[Close]列の値)の自然対数(ln)を取ります。日付の列と対数値の列の2列をコピーして、新しいcsvファイルを作成します。ファイル名をnikkei_data.csv とします。
作成したcsvファイルをpandasモジュールを使って読み込みます。Jupyter notebookを開いて、以下のコードをコピペしてください。ここでは、1年分のデータを使用しています。このコードの保存されたディレクトリにnikkei_data.csvファイルを置いてください。 データをロードするときに最初の行は除外できます。ダウンロードしたデータセットはフッタ情報も持ちますが、これも pandas.read_csv() への skipfooter 引数を (3 フッタ行のための) 3 に設定することで除外可能です。データセットは Pandas dataframe としてロードします。そして dataframe から NumPy 配列を取り出して整数値を浮動小数点値に変換します。(このデータではこの部分は必要ありませんが。)以下のコードは、このサイトで提供されたコードに多くを負っています。
import pandas
import matplotlib.pyplot as plt
dataframe = pandas.read_csv('nikkei_data.csv', usecols=[1], engine='python', skipfooter=3)
dataset = dataframe.values
dataset = dataset.astype('float32')
plt.plot(dataset)
plt.show()
このコードを実行すると、日経平均株価の時系列データがプロットされます。次に、TensorFlow を用いてネットワークを構成します。データの数値を[0,1]の範囲に正規化します。以下のコードは、このサイトを参考にしています。
import numpy as np import matplotlib.pyplot as plt import math from keras.models import Sequential from keras.layers import Dense, LSTM from sklearn.preprocessing import MinMaxScaler from sklearn.metrics import mean_squared_error # fix random seed for reproducibility np.random.seed(7) # normalize the dataset scaler = MinMaxScaler(feature_range=(0, 1)) dataset = scaler.fit_transform(dataset) # split into train and test sets train_size = int(len(dataset) * 0.7) test_size = len(dataset) - train_size train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:] print(len(train), len(test))
トレーニングデータとテスト用データに分割された個数が表示されます。新しいデータセットを作成する関数を定義します。この関数は 2 つの引数を取ります。 dataset=新しいデータセットに変換することを望む NumPy 配列 、 maxlen=次の時間区間を予測するために入力変数として使用する前の時間ステップの数、通常、sequence_lengthなどと表記されることもあります。次のタイムステップの予測をするために複数の、直近のタイムステップを使用できるようにプログラムを修正することもできます。例えば、現在の時間 (t) が与えられてシークエンスの次の時間 (t+1) における値を予測したい場合、入力変数として現在時間 (t)以前のデータ、そして 2 つの前の時間 (t-1) と (t-2)以前のデータ を使用することができます。maxlen=3とすると、X が与えられた時間 (t, t-1, t-2) における株価、Y が時間 (t + 1) における株価であるようなデータセットを作成します 。入力変数は時刻 t-2, t-1, t の3次元のsequence数x3行列で、出力変数は t+1 での値(1次元スカラー)です。
# convert an array of values into a dataset matrix
def create_dataset(dataset, maxlen:
dataX, dataY = [], []
for i in range(len(dataset)-maxlen-1):
a = dataset[i:(i+maxlen), 0]
dataX.append(a)
dataY.append(dataset[i + maxlen, 0])
return np.array(dataX), np.array(dataY)
# reshape into X=t and Y=t+maxlen
maxlen = 3
trainX, trainY = create_dataset(train, maxlen)
testX, testY = create_dataset(test, maxlen)
print (trainX[:10,:])
print (trainY[:10])
# reshape input to be [samples, time steps, features]
trainX = np.reshape(trainX, (trainX.shape[0], 1, trainX.shape[1]))
testX = np.reshape(testX, (testX.shape[0], 1, testX.shape[1]))
print(trainX[:10,:])
データtrainX[:10,:]の例が表示されます。この問題に対する LSTM ネットワークを構成して、 fit する準備ができました。ネットワークは 1 入力を持つ可視層、4つの LSTM ブロックを持つ隠れ層LSTM(4, input_shape=(1, maxlen))、そして単一の値予測を行なう出力層Dense(1)を持ちます。デフォルトの sigmoid 活性化関数が LSTM ブロックのために使用されます。ネットワークは 100 エポック訓練されてサイズ 1 のバッチが使用されます
# create and fit the LSTM network model = Sequential() model.add(LSTM(4, input_shape=(1, maxlen))) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=2)
このコードを実行すると、エポックごとの結果が表示されます。
学習したモデルを用いて、予測を行います。予測されたデータを元の配列形式に戻してからinverse_transform()、誤差の計算を行います。
# make predictions
trainPredict = model.predict(trainX)
testPredict = model.predict(testX)
# invert predictions
trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform([trainY])
testPredict = scaler.inverse_transform(testPredict)
testY = scaler.inverse_transform([testY])
# calculate RMSE( root mean squared error)
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
# shift train predictions for plotting
trainPredictPlot = np.empty_like(dataset)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[maxlen:len(trainPredict)+maxlen, :] = trainPredict
# shift test predictions for plotting
testPredictPlot = np.empty_like(dataset)
testPredictPlot[:, :] = np.nan
testPredictPlot[len(trainPredict)+(maxlen*2)+1:len(dataset)-1, :] = testPredict
# plot baseline and predictions
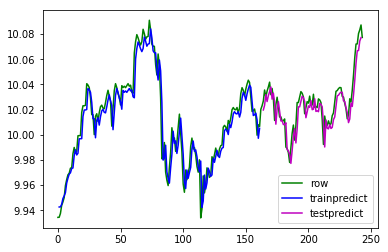
plt.plot(scaler.inverse_transform(dataset), color ="g", label = "row")
plt.plot(trainPredictPlot,color="b", label="trainpredict")
plt.plot(testPredictPlot,color="m", label="testpredict")
plt.legend()
plt.show()
以下の様なグラフが得られます。

この結果を見ると、予測値はデータ値に時間的に若干遅れています。予測は現実の後追いをしている感じです。create_dataset() 関数における maxlen 引数を 3 から 任意の数値、例えば、20 に増やすことで予測を修正できます。LSTMレイヤーの隠れ層のニューロン数を増加させることで、例えば、20に変化させることで、予測の修正をすることもできます。
今まで見てきたように、従来、 自然言語処理 における Deep Learning アルゴリズムと言えば、 LSTM や GRU といった RNN (Recurrent Neural Network) でした。ところが、2017年6月、 "Attention Is All You Need" という強いタイトルの論文が Google から発表され、機械翻訳のスコアを既存の RNN モデル等から大きく引き上げます。論文”Transformer: A Novel Neural Network Architecture for Language Understanding”において、RNN や CNN を使わず Attention のみ使用したニューラル機械翻訳 Transformer が提案されました。
BERT(Bidirectional Encoder Representations from Transformers)は、Transformerのアルゴリズムを活用した双方向的エンコード表現による言語処理のアプリで、2018年10月にGoogle AI Languageの研究者が論文で発表したものです。この論文において質疑応答(SQuAD)と自然言語推論(MNL1)、Microsoft Research Paraphrase Corpus (MRPC)などの様々な自然言語処理の幅広いタスクにおいて最先端の結果が公表されたことにより、言語処理の機械学習研究に大きな影響を与えました。
自然言語処理の分野では、LSTM などのアルゴリズムに代わり Pytorch_transformer などのアルゴリズムが主流になると思われます。なので、 LSTM の話はこれでおしまいにします。
Pytorch_transformer による自然言語処理のページに行く