Recursive Neural Network(https://deepinsider.jp/tutor/introtensorflow/whatisrnnから引用)
|
自然言語データや時系列データは入力変数の中に系列依存関係の複雑さをもつので、このような系列依存データを用いた推論や予測問題は機械学習問題の中でも困難なもので、画像識別や物体検出問題よりも一段と複雑な課題になります。
系列連鎖を持つデータの予測においては、各入力信号を独立した入力ではなく、ある種の関係性をもつ一連の入力データとして取り扱い、これらの入力信号に対応した一連の出力データとして出力することが必要となります。単純なニューラルネットワークでは、推論結果は最後の層からのアウトプットとしてのみ出力されるため、一連の入力に対して一連の出力という対応関係で出力することはできません。この課題に応えるために、ネットワークの出力を別のネットワークの入力として利用するような再帰的構造を持ったモデルを構築する必要があります。ここに、ある層の出力は、次の層の入力として利用されるだけでなく、その後の複数の層の入力データとしても利用できるネットワークモデルが登場します。こうしたモデルを Recurisive Neural Network と呼びます。多層パーセプトロン・モデルにフィードバック・ループを組み込んだ構造をしていると理解できます。
このような Recursive Neural Network の一つのバージョンに Recurrent Neural Network (RNN) と呼ばれるモデルがあります。さらに、 Recurrent Neural Network の拡張バージョンに、Long Short-Term Memory (LSTM) と呼ばれるモデルが登場します。歴史的には、LSTM の第1世代は、AlexNetなどの CNN モデルの登場よりも15年以上前の、LeNetと同時期の1997年に、Hochreiter と Schmidhuber の論文で発表されました。その後、多数の研究者の努力によって開発がつづけられて、音声識別などの自然言語処理や時系列データの分析に応用されるようになっています。
画像認識分野においては、性能向上を目的として、Alexnet(8層、2012年)、VGG(16または19層、2014年)、GoogLeNet(22層、2014年)、ResNet(152層、2015年)と年を追うごとにその層数を増加させてきました。しかし、層を増やせば増やすほど学習精度が向上するわけではないので、緻密なアーキテクチャの構築によって層数の増加、精度向上が図られました。一方で、RNNそのもののネットワーク構造はフィードバック・ループという再帰的ネットワークを1つ持つだけの単純な構造をしています。これを時系列方向に展開すると、その総数は時系列の長さに比例します。したがって、多くの時系列データは数百ステップ以上の長期のステップを扱うので、RNNの方が深い層数を扱っているとも言えます。
このページでは、RNN および LSTM の構造を簡単に説明して、自然言語における感情分析やトピック類似性などの推測問題、時系列データの予測問題を処理するために、 RNN 及び LSTM ネットワークをどのように実装できるかを説明します。TensorFlow で RNN のコードを使用するための説明は、この公式サイトにあります。PyTorch で RNN のコードを使用した名前の言語分類は公式サイトの Classifying Names with a Character-Level RNN にあります。
このページでは、主に、PyTorch を用いた RNN と LSTM モデルの Python 実装の例を取り上げます。このページで採り上げた例に対応するコードは、この GitHub Repo アップロードしてありますので、ご利用ください。すべて Google Colab で実行できる形になっています。
Last updated: 2020.4.22(first uploaded 2019.4.26)
再帰型ニューラルネットワーク(RNN)モデル |
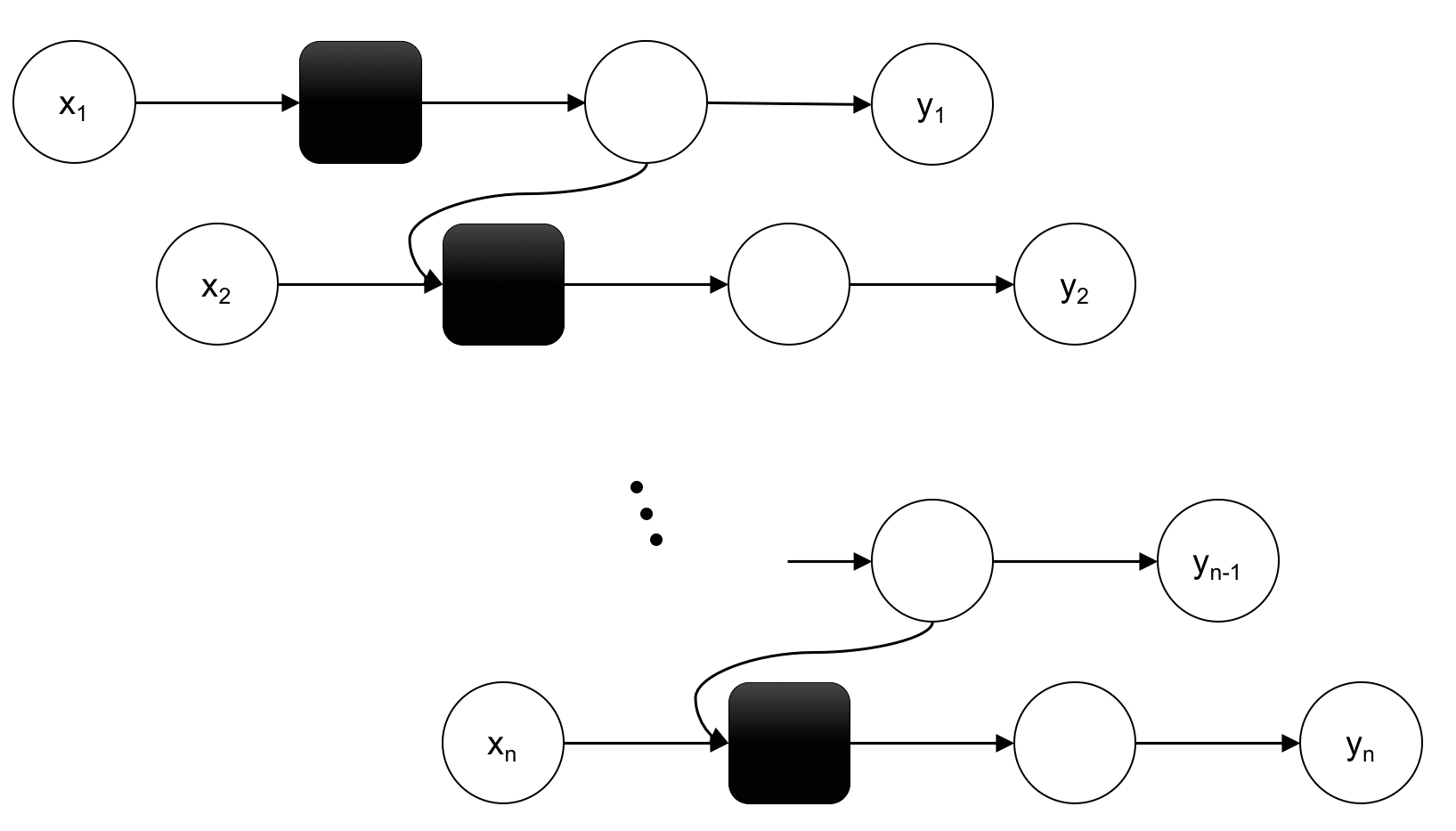
RNNの大きな特徴の一つは、時系列上のある時点の入力信号が、それ以降の出力データに影響を及ぼす、ということです。過去の情報を基に予測できるということにあります。言い換えると、隠れ層の値を再び隠れ層に入力するというネットワーク構造にしたのが、RNNです。下の図は、この隠れ層に戻すという操作を、時間軸方向に展開した図になります。入力信号の時系列データを
\[ x_1, x_2, . . , x_n \] とし、それに対応した出力データを \[ y_1, y_2, . . . ,y_n \]とします。以下の図のように処理されます。

Recursive Neural Network(https://deepinsider.jp/tutor/introtensorflow/whatisrnnから引用)
Recursive Neural Networkの中でも、図のように隠れ層同士の結合が時系列に沿って直線的であり、かつその隠れ層が同一構造であるような場合を「RNN」と言います。 \( x_1 \) の矢印をたどっていくと、 \( y_1 \)から\( y_n \) まで到達する。つまり \( y_1 \)から\( y_n \) に影響する。同様に\( x_2 \)は\( y_2 \)から\(y_n \) に影響しています。
RNNの隠れ層において、再帰的に出現する同一のネットワーク構造のことをセル(cell)と呼びます。図の中の黒く塗りつぶした四角形の部分です。時刻\( t \)に対応する、このセルを含む隠れ層の出力を\( h_t \)とし、入力信号を\( x_t \)と表記します。このとき、隠れ層の出力は
\[ h_t = \tanh (h_{t-1} W_h + x_t W_x + b) \]と計算されます。活性化関数は通常はSigmoid 関数ですが、ここでは、\( \tanh \)関数を使用しています。RNN には重みが2種類あり、入力信号を変換する重み\( W_x \)と、一つ前の時刻での隠れ層の出力\( h_{t-1} \)を次の時刻の出力に変換するための重り\( W_h \)です。\( b \)はバイアスです。\(h_t, x_t \)は行ベクトルとします。
RNNは、時間的構造の表現を取り扱えるので、自然言語や時系列データなど、連続性のあるデータの識別や生成に使われています。機械翻訳や、音声認識してテキスト化するサービス、文章の生成などで使用されています。原論文は、このサイトからダウンロードできます。
RNN を Pytorch を用いて実装する例を取り上げます。Classifying Names with a Character-Level RNNに沿って説明します。RNN の簡単化した図式を示します。
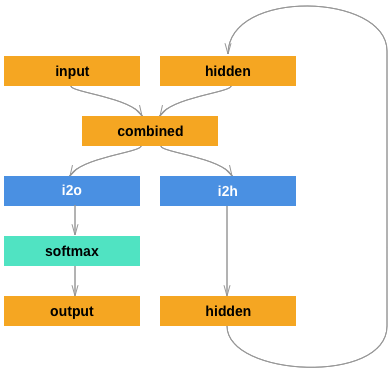
このようなグラフで表現される RNN モデルは次のコードで作成できます。活性化関数として softmax 関数が採用されています。
import torch.nn as nn
class RNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(RNN, self).__init__()
self.hidden_size = hidden_size
self.i2h = nn.Linear(input_size + hidden_size, hidden_size)
self.i2o = nn.Linear(input_size + hidden_size, output_size)
self.softmax = nn.LogSoftmax(dim=1)
def forward(self, input, hidden):
combined = torch.cat((input, hidden), 1)
hidden = self.i2h(combined)
output = self.i2o(combined)
output = self.softmax(output)
return output, hidden
def initHidden(self):
return torch.zeros(1, self.hidden_size)
n_hidden = 128
rnn = RNN(n_letters, n_hidden, n_categories)
...
output, hn =rnn(input, h0)
上記のように RNN のネットワークを明示的に作成する必要はありません。モジュール化した 組み込み RNN モデルを使用することもできます。以下のように呼び出して、使用します。
import torch import torch.nn as nn n_input = 10 n_hidden = 20 n_layers=2 rnn = nn.RNN(n_input, n_hidden, n_layers) input = torch.randn(5, 3, 10) h0 = torch.randn(2, 3, 20) output, next_hidden = rnn(input, h0)
組み込みモジュール nn.RNN では、デフォルトで、nonlinerarity に \( \tanh \)関数を使用しています。このモジュールを用いて、センテンスの学習から一つの単語の入力から次のくるべきセンテンスを予測するプログラムの例を、Google Colab にアップしておきました。実行してみて下さい。使用された文章の例は以下の通りです。
text = ['hey guys', 'good morning', 'how are you','fine, and you', 'i am fine too','have a nice day']
# Join all the sentences together and extract the unique characters from the combined sentences
chars = set(''.join(text))
# Creating a dictionary that maps integers to the characters
int2char = dict(enumerate(chars))
# Creating another dictionary that maps characters to integers
char2int = {char: ind for ind, char in int2char.items()}
Model の部分は以下のように作成されています。
class Model(nn.Module):
def __init__(self, input_size, output_size, hidden_dim, n_layers):
super(Model, self).__init__()
# Defining some parameters
self.hidden_dim = hidden_dim
self.n_layers = n_layers
#Defining the layers
# RNN Layer
self.rnn = nn.RNN(input_size, hidden_dim, n_layers, batch_first=True)
# Fully connected layer
self.fc = nn.Linear(hidden_dim, output_size)
def forward(self, x):
batch_size = x.size(0)
#Initializing hidden state for first input using method defined below
hidden = self.init_hidden(batch_size)
# Passing in the input and hidden state into the model and obtaining outputs
out, hidden = self.rnn(x, hidden)
# Reshaping the outputs such that it can be fit into the fully connected layer
out = out.contiguous().view(-1, self.hidden_dim)
out = self.fc(out)
return out, hidden
def init_hidden(self, batch_size):
# This method generates the first hidden state of zeros which we'll use in the forward pass
hidden = torch.zeros(self.n_layers, batch_size, self.hidden_dim).to(device)
# We'll send the tensor holding the hidden state to the device we specified earlier as well
return hidden
次にモデルに学習させます。
# Instantiate the model with hyperparameters
model = Model(input_size=dict_size, output_size=dict_size, hidden_dim=12, n_layers=1)
# We'll also set the model to the device that we defined earlier (default is CPU)
model = model.to(device)
# Define hyperparameters
n_epochs = 100
lr=0.01
# Define Loss, Optimizer
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
# Training Run
input_seq = input_seq.to(device)
for epoch in range(1, n_epochs + 1):
optimizer.zero_grad() # Clears existing gradients from previous epoch
#input_seq = input_seq.to(device)
output, hidden = model(input_seq)
output = output.to(device)
target_seq = target_seq.to(device)
loss = criterion(output, target_seq.view(-1).long())
loss.backward() # Does backpropagation and calculates gradients
optimizer.step() # Updates the weights accordingly
if epoch%10 == 0:
print('Epoch: {}/{}.............'.format(epoch, n_epochs), end=' ')
print("Loss: {:.4f}".format(loss.item()))
学習したモデルを用いて、推論をさせます。
def predict(model, character):
# One-hot encoding our input to fit into the model
character = np.array([[char2int[c] for c in character]])
character = one_hot_encode(character, dict_size, character.shape[1], 1)
character = torch.from_numpy(character)
character = character.to(device)
out, hidden = model(character)
prob = nn.functional.softmax(out[-1], dim=0).data
# Taking the class with the highest probability score from the output
char_ind = torch.max(prob, dim=0)[1].item()
return int2char[char_ind], hidden
def sample(model, out_len, start='good'):
model.eval() # eval mode
start = start.lower()
# First off, run through the starting characters
chars = [ch for ch in start]
size = out_len - len(chars)
# Now pass in the previous characters and get a new one
for ii in range(size):
char, h = predict(model, chars)
chars.append(char)
return ''.join(chars)
sample(model, 15, 'how')
---- result
'how are you '
'how' の後に続くセンテンスを予測しました。結果は正しいです。
LSTM(Long Short Term Memory)モデル |
LSTMは現在Google Voiceの基盤技術をはじめとした最先端の分野でも利用されていますが、その登場は1997年とそのイメージとは裏腹に長い歴史を持つモデルです。LSTM(Long short-term memory)は、RNN(Recurrent Neural Network)の拡張として登場した時系列データ(sequential data)に対するモデル、あるいは構造(architecture)の1種です。なので、LSTM(Long Short-Term Memory)はRNNの欠点を解消し、長期の時系列データを学習することができる強力なモデルです。その名は、Long term memory(長期記憶)とShort term memory(短期記憶)という神経科学における用語から取られています。LSTMはRNNの中間層のユニットをLSTM blockと呼ばれるメモリセルと3つのゲートを持つブロックに置き換えることで実現されています。LSTMブロックの中身は概略的には下のグラフの様になっています。
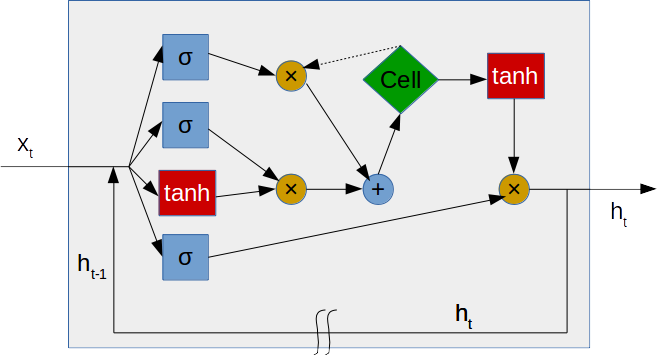
LSTMはデータ\( x_t \)を受け取ると、1ステップ前の自身の出力\( h_{t−1} \)と\( x_t \)を使い内部で計算を行い、今回の出力\( h_t \)とします。さらに、\( h_t \)は次回の出力\( h_{t+1} \)を使うためにも使います。これが、過去の出力を自身の入力にフィードバックしていた原始的なリカレントネットワークの隠れ層の部分です。入力側には、4つの矢印で表記されたエッジがあります。もっとも下の矢印(ゲート)から入る経路がこれです。output gate と呼ばれます。そこでの計算は
\[ o_t=\sigma (x_t \cdot W_o+h_{t−1} \cdot R_o+b_o) \]となります。ここで、\( \sigma \)は活性化関数です。\( W_o, R_o \)は重み行列です。
入力側の一番上位に位置する矢印が forget gate と呼ばれるゲートで、そこから入った信号は
\[ f_t=\sigma (x_t \cdot W_f + h_{t-1} \cdot R_f + b_f) \]の計算で処理されて、メモリセルの方向に送られます。メモリセルにあるデータ(\( c_{t-1} \))を用いて
\[ c_{t−1}\otimes f_t \]という計算が行われます。ここで、\( \otimes \)はアダマール積を表記します。上から2番目の矢印が input gate と呼ばれるゲートで、
\[ i_t=\sigma (x_t \cdot W_i + h_{t-1} \cdot R_i + b_i) \]と処理されます。その下のゲートから入った信号は
\[ z_t=\tanh (x_t \cdot W_z + h_{t-1} \cdot R_z + b_z) \]と計算されます。この計算結果は input gate から送られた情報とともに、
\[ c_t=i_t \otimes z_t+c_{t−1} \otimes f_t \]という計算で処理されます。このデータがメモリセルに追加されます。ここで、\( c_{t-1} \)は、メモリセルにある過去、時刻\( t-1 \)のデータを表します。メモリーセルから出てくる点線は\( c_{t−1} \)という前の時刻の値を出しています。メモリセルは、\( c_t \)という値を次の計算に渡したり、\( c_{t−1} \)という値を保持するという役割を持っているだけで、特別な計算はしません。最後に、LSTMの出力が
\[ h_t=o_t \otimes \tanh(c_t) \]と計算されます。
LSTMのその最も大きな特長は、従来のRNNでは学習できなかった長期依存(long-term dependencies)を学習可能であるところにあります。例えば、下のような時系列
\[ (z,x_1,x_2,⋯,x_p,z) \]を受け取り、次のステップ値の入力を予測するような学習器を考えます。\( z \)が入力されたのち\( p \)ステップ後に再び\( z \)を受け取っています。この系列を正しく学習するためには、最初の要素の情報を少なくともp ステップ維持する機能を持つようにネットワークの重みを更新する必要があります。通常のRNNでも数十ステップの短期依存(short-term dependencies)には対応できるのですが、1000ステップのような長期の系列は学習することができませんでした。LSTMはこのような系列に対しても適切な出力を行うことができます。
Pytorch を用いて LSTM を Python 実装する例を見てみましょう。以下のコードは最も簡単な例です。
import torch
import torch.nn as nn
batch_size = 20
seq_len = 10 # length of sequence
input_size = 2
hidden_size = 4 # num of layers
# 入力データのサンプル
input_seq = torch.randn(batch_size, seq_len, input_size)
print('input sequence:', input_seq.shape)
# ネットワークの定義
net = nn.LSTM(input_size, hidden_size, num_layers=2, batch_first=True)
# 順伝播
output_seq, _ = net(input_seq)
# 出力データの確認
print('output sequence:', output_seq.shape)
---- result
input sequence: torch.Size([20, 10, 2])
output sequence: torch.Size([20, 10, 4])
batch_first=Trueと設定すると、LSTM の入力が(batch_size, seq_len, input_size)であるとき、出力 y は (batch_size, seq_len, hidden_size) となります。これはシークエンス(系列)の長さが同一のデータが20個揃っているケースを想定しています。一般的には同一のシークエンスの長さに揃えてから、この処理を行います。
もう少し複雑な LSTM モデルの Python 実装の例を見てみましょう。実装するのは、「sin波の予測」です。直前の50ステップかを入力することで、次のsinの値が何になるかを予想しようというものになります。 より具体的には、LSTMにノイズ混じりのsin波の値を50ステップ分(t = t_1, t_2, ... , t_50)入れて、次の値(t = t_51)を最終出力として得るようなモデルを、教師あり学習で学習します。このコードは、 この Google Colab にアップロードしてあります。次のようなDataset 関数を作りましょう。
pytorchのLSTMでは、入力テンソルは3次元であると規定されており、batch_size=true なので、具体的な形状は(Batch_Size ,Sequence_Length,Input_Size) になります。今回の例では、Sequnece_size(入力時系列の長さ)= 50、Vector_Size(入力ベクトルサイズ)= 1のテンソルを入力することになります。sin波が出るだけなので、少しノイズを乗せてみましょう。
import math
import numpy as np
def mkDataSet(data_size, data_length=50, freq=60., noise=0.02):
"""
params
data_size : データセットサイズ
data_length : 各データの時系列長
freq : 周波数
noise : ノイズの振幅
returns
train_x : トレーニングデータ(t=1,2,...,size-1の値)
train_t : トレーニングデータのラベル(t=sizeの値)
"""
train_x = []
train_t = []
for offset in range(data_size):
train_x.append([[math.sin(2 * math.pi * (offset + i) / freq) + np.random.normal(loc=0.0, scale=noise)] for i in range(data_length)])
train_t.append([math.sin(2 * math.pi * (offset + data_length) / freq)])
return train_x, train_t
入力データの前処理をします。
def mkRandomBatch(train_x, train_t, batch_size=10):
"""
train_x, train_tを受け取ってbatch_x, batch_tを返す。
"""
batch_x = []
batch_t = []
for i in range(batch_size):
# idx = np.random.randint(0, len(train_x) - 1)
idx = i
batch_x.append(train_x[idx])
batch_t.append(train_t[idx])
return torch.tensor(batch_x), torch.tensor(batch_t)
モデルを作成します。
import torch
import torch.nn as nn
class Predictor(nn.Module):
def __init__(self, inputDim, hiddenDim, outputDim):
super(Predictor, self).__init__()
self.rnn = nn.LSTM(input_size = inputDim,
hidden_size = hiddenDim,
batch_first = True)
self.output_layer = nn.Linear(hiddenDim, outputDim)
def forward(self, inputs, hidden0=None):
output, (hidden, cell) = self.rnn(inputs, hidden0) #LSTM層
output = self.output_layer(output[:, -1, :]) #全結合層
return output
モデルの学習をします。
training_size = 10000
test_size = 1000
epochs_num = 300
hidden_size = 5
batch_size = 100
train_x, train_t = mkDataSet(training_size)
test_x, test_t = mkDataSet(test_size)
model = Predictor(1, hidden_size, 1)
criterion = nn.MSELoss()
optimizer = SGD(model.parameters(), lr=0.01)
for epoch in range(epochs_num):
# training
running_loss = 0.0
training_accuracy = 0.0
for i in range(int(training_size / batch_size)):
optimizer.zero_grad()
data, label = mkRandomBatch(train_x, train_t, batch_size)
output = model(data)
loss = criterion(output, label)
loss.backward()
optimizer.step()
running_loss += loss.data
training_accuracy += np.sum(np.abs((output.data - label.data).numpy()) < 0.1)
#test
test_accuracy = 0.0
for i in range(int(test_size / batch_size)):
offset = i * batch_size
data, label = torch.tensor(test_x[offset:offset+batch_size]), torch.tensor(test_t[offset:offset+batch_size])
output = model(data, None)
test_accuracy += np.sum(np.abs((output.data - label.data).numpy()) < 0.1)
training_accuracy /= training_size
test_accuracy /= test_size
print('%d loss: %.3f, training_accuracy: %.5f, test_accuracy: %.5f' % (
epoch + 1, running_loss, training_accuracy, test_accuracy))
1 loss: 46.836, training_accuracy: 0.06730, test_accuracy: 0.06800 2 loss: 43.583, training_accuracy: 0.08000, test_accuracy: 0.06800 3 loss: 39.512, training_accuracy: 0.08720, test_accuracy: 0.08500 4 loss: 30.553, training_accuracy: 0.09230, test_accuracy: 0.08500 5 loss: 16.740, training_accuracy: 0.11940, test_accuracy: 0.10200 6 loss: 8.729, training_accuracy: 0.13410, test_accuracy: 0.12900 7 loss: 5.894, training_accuracy: 0.15910, test_accuracy: 0.15300 8 loss: 4.659, training_accuracy: 0.17390, test_accuracy: 0.15300 9 loss: 3.931, training_accuracy: 0.19170, test_accuracy: 0.17500 10 loss: 3.433, training_accuracy: 0.21560, test_accuracy: 0.18800 ...
結果を見てみましょう。
import matplotlib.pyplot as plt data, label = mkRandomBatch(test_x, test_t, batch_size) output=model(data) plt.figure() plt.plot(output.data, color="r", label="predict_data") plt.plot(label.data, color="b", label="row_data") plt.legend() plt.show()
Colab のコードを実行して、確認してみて下さい。以下のように予測されたサイン波形が表示されます。
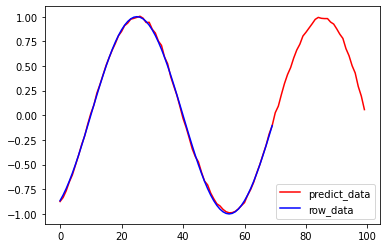
Tensorflow.Keras で LSTM モデルを用いて、sin波の時系列予測問題を採り上げた例は この Colab にアップロードしtれあります。利用して下さい。
時系列データの代表例として想定できるものは、電波、音声波形、株価指数、為替レート、気温変化などです。通念では時系列データとして想定されないものとして、文章(単語列)などがあります。電波の波形なら一定の時間間隔でのサンプル値になりますし、文章なら単語を前から並べたときの番号になります。文章生成ならば、今までの単語列を入力として、もっともらしい次の単語を予測することが課題となります。正しい文章
the monkey ate the appleを繰り返しLSTMに覚えさせる(重みベクトルを更新する)ことで、"monkey"の後に"ate"が来るようなルールを学習することができます。音素・音声認識の場合、今までの音声波形(orその特徴量)を入力として、その時点で発話されている音素を予測することが課題になります。
LSTM を用いた時系列分析
自然言語処理のページへ
トップ・ページに戻る