Python Tutorials : Applications

Welcome to Mashykom WebSite

PythonのTutorials - Programing & Applications

　Pythonはさまざまな分野のアプリケーションで使われている、極めてパワフルな動的プログラミング言語です。機械学習、ディープ・ラーニングやデータサイエンスなどの分野では必須の言語となっています。ロボティクスで使用されるシングルボード・コンピュータのRaspberry Piでは組み込み言語として必須の役割をします。

　Pythonをインストールしていること、Jupyter Notebookを用いることを前提にしています。したがって、Python及びJupyter Notebookのインストールのページを読んでいることを前提にします。

　このページに掲載されるスクリプト類の動作は、MacOS10.12以降及びUbuntu 16.04以降で実証しています。Windowsでも問題なく作動すると思います。 Ubuntu Mate をインストールしたRaspberry Piで'ipython' を使用するときは、


$ sudo apt install ipython3

とpython3 用の'ipython3' をインストールします。<\p>


$ ipython3

と入力して、python3 を起動します。Raspbian Stretch をインストールしたRaspberry Piでは、デスクトップ画面のプログラミング・メニューバーからpython3(IDLE)を起動できます。Jupyter notebookをインストールできない場合には、スクリプトに名前をつけて（例えば、example_script といファイル名で）、一旦保存してから、スクリプトの保存されているディレクトリに移動して、


$ python3 example_script

とコマンドを入力して、実行してください。

　以下で使用するサンプルコードはこの github にあります。経済モデルのシミュレーションで使用されたコードは、このColaboratoryにアップしました。自由に活用ください。

（Last updated:2021/1/18)

経済成長のSolowモデルのシミュレーション

　以下は、マクロ経済学の知識が要求されます。興味のない読者はスキップしてください。経済学の経済成長理論における基本モデルのシミュレーションを取り上げます。最初に、新古典派モデルの典型であるSolowモデルを考えます。このモデルではマクロ経済で産出される財は均質な財と仮定されています。いわゆる1部門経済成長のモデルです。

　生産関数は \[ Y_t = A_t F(K_t, H_t), \] で与えられる。ここで、\(Y_t\)は時刻\(t\)における経済全体の総生産量、\(A_t\)は時刻\(t\)での生産技術水準、\(K_t\)は時刻\(t\)での資本ストック、\(H_t\)は生産に投入された労働量を表現する。生産関数は一次同次であると仮定する。総生産量を労働者一人当たりに変換すると、 \[ y_t = \frac{Y_t}{H_t} = A_t F(\frac{K_t}{H_t}, \frac{H_t}{H_t}) = A_t F(k_t, 1) \equiv A_t f(k_t) , \] となる。ここで、\(k_t\)は一人当たり資本ストックである。労働力が一定の成長率\(n\)で拡大すると仮定するならば、\(H_{t+1} = (1+n)H_t\)が成立する。また、資本ストックは蓄積方程式 \[ K_{t+1} = (1- \delta)K_t + I_t \] に従って成長する。\(\delta\)は減価償却率、\(I_t\)は時刻\(t\)での粗投資額である。この式から、一人当たり資本の蓄積は \[ k_{t+1} = \frac{(1- \delta)k_t + i_t}{1+n} \] に従う。ここで、\(i_t\)は労働者一人当たり粗投資である。貯蓄が生産量の一定割合で行われると仮定できるとうする。つまり、\(s_t = \sigma y_t\)と仮定する。\(\sigma\)は労働者一人当たりの貯蓄率と理解される。\(i_t = s_t\)を資本の蓄積方程式に代入すると、 \[ k_{t+1} = \frac{(1- \delta)k_t + \sigma A_t f(k_t)}{1+n} \] が得られる。

生産関数を\(f(k_t) = k_t^{\theta}\)と簡単化する。生産技術へのショックは \[ A_t = \bar{A}e^{\epsilon _t} \] で表現される。ここで、\(\epsilon_t\)は平均値ゼロの正規分布に従う。このモデルをシミュレーションする。パラメータ値として、\(\bar{A} = 1, \: n = 0.02, \: \delta =0.1, \: \theta = 0.36, \: \sigma =0.2 \)を採用した。

　シミュレーションのスクリプトは以下の通りです。

# This program shows the simulation results for the simple Solow model of economic growth.
'''
     the production function f(K)=A K^theta
     the expression for the technology shock = exp(epsilon_t): the standard error =volat
     the rate of population growth = n
     the depreciation rate = delta
     the saving rate = sigma
'''
from numpy import *
import matplotlib.pyplot as plt

# set up the parameters' value.
T=120
delta=0.1
A=1.0
sigma=0.2
n=0.02
theta=0.36
volat=0.2

# compute the steady state of the economy.
B=(1+theta*n-delta*(1-theta))/(1+n)
C=(delta+n)/(1+n)
X_ss=((n+delta)/(sigma*A))**(1/(theta-1))
print ('The steady state level of the output is', X_ss)

icase=3 # icase=the number of simulations 
K=zeros((icase,T))
X=zeros((icase,T))
k=zeros((icase,T))
R=zeros((icase,T))
for i in arange(icase):
    K[i,0]=2.0
    X[i,0]=2.0
    k[i,0]=0.0

# compute the trajectories of the economy given the exogenous shocks.
for i in arange(icase):
    for t in arange(T-1):
        R[i,t]=volat*random.randn(1)
        K[i,t+1]=((1-delta)*K[i,t]+sigma*A*exp(R[i,t])*K[i,t]**(theta))/(1+n)
        k[i,t+1]=B*k[i,t]+C*R[i,t]
        X[i,t+1]=X_ss*exp(k[i,t+1])

time=arange(0,T)

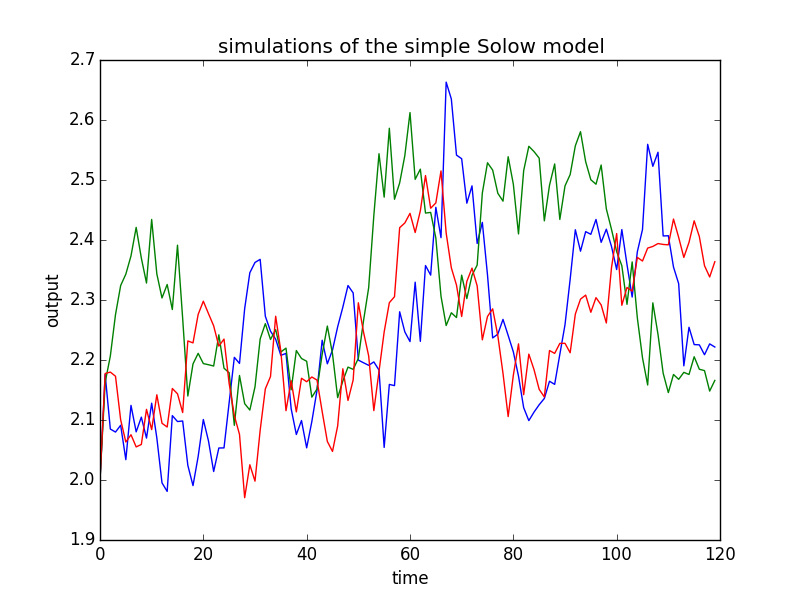
plt.title('simulations of the simple Solow model')
plt.plot(time, X[0,:],time,X[1,:],time, X[2,:])
plt.xlabel('time')
plt.ylabel('output')
plt.show()

このスクリプトを実行すると、3回のシミュレーションが実行され、以下のグラフが得られます。

Solow_model_demo

DSGEモデルのシミュレーション:Hansen model

　次に、1980年代に登場した内生的経済成長理論の基礎となる新新古典派の経済成長モデルを取り上げます。これらのモデルの解説については、「経済変動の動学的確率的一般均衡モデル」のPDFファイルを参照ください。python コードを用いたシミュレーション結果が説明されています。

　Romer、Lucas、Barro達が代表的な理論家ですが、その初期の理論となるHansenモデルを考えます。シミュレーション用のスクリプトは結構な長さになります。以下はマクロ経済学の知識が要求されますので、行列の固有値（線形代数）に関する知識がない読者はスクリプトの内容はスキップしてください。中身を具体的に理解したい読者はReal Business Cycleに関するテキストを、例えば、George McCandless(2008), The ABCs of RBCs: An introduction to Dynamic Macroeconomic Models, Harvard University Press.を参照してください。

代表的家計は生涯にわたる効用

\[ E_0[\Sigma _{t=0}^{\infty} \beta^t u(C_t,H_t)] \]

　を最大にするような消費\({C_t}\)と労働供給\({H_t}\)を選択する。レジャー\(L_t\)は\(L_t =1-H_t\)で与えられる。言い換えると、家計の有効な使用可能時間を1に規格化している。ここで、変数、例えば、\(C_t\)の表現における下添え字\(t\)は時刻を表す。\(E_0\)は初期時点での条件付き期待値オペレータである。生産関数を\(f(\lambda _t, K_t, H_t)\)で表現する。\(\lambda_t \)は時刻\(t\)における生産技術に対する外的なショックの大きさを表し、\(K_t\)は資本投入量、\(H_t\)は労働投入量である。資本ストックは

蓄積方程式 \[ K_{t+1} = (1-\delta) K_{t-1} + I_t \] に従う。ここで、\(I_t\)は時刻\(t\)での投資、\(\delta\)は資本の減価償却率である。生産された価値は消費と投資に配分されるので、 \[ f(\lambda _t, K_t, H_t) = C_t + I_t \] が成立する。

　モデルの数値的な挙動を調べるに当たって \[ Y_t = f(\lambda _t, K_t, H_t) =\lambda _t K_t^{\theta} H_t^{1-\theta}, \quad u(C_t,H_t)=\mbox{ln} C_t + A \; \mbox{ln} (1-H_t) \] と具体的な関数形を与えるとき、第１階条件は \begin{eqnarray} \frac{1}{C_t} &=& \beta E_t[ \frac{\theta \lambda _{t+1} K_{t+1}^{\theta-1} H_{t+1}^{1-\theta} + (1- \delta) }{C_{t+1}}|\lambda _t], \label{HS1}\\ A C_t &=& (1-\theta)(1-H_t)\lambda _t k_t^{\theta} H_t^{-\theta} \label{HS2} \end{eqnarray} と簡単化される。また、 \[ C_t = \lambda _t K_t^{\theta} H_t^{1-\theta} + (1- \delta)K_t - K_{t+1} \] が成立している。

　要素市場が完全競争市場であれば、資本の限界生産は資本のレンタル価格(利子率)\(r\)に等しく、労働の限界生産は賃金率\(w\)に等しくなる。 \[ r_t = \theta \lambda _t K_t^{\theta-1} H_t^{1-\theta}=\theta \frac{Y_t}{K_t}, \quad w_t = (1-\theta) \lambda _t K_t^{\theta} H_t^{-\theta} = (1-\theta)\frac{Y_t}{H_t} . \] 　これらの条件を用いると第１階条件は \begin{eqnarray*} \frac{1}{C_t} &=& \beta E_t[ \frac{r_{t+1} + (1- \delta) }{C_{t+1}}|\lambda _t], \\ A C_t &=& (1-H_t)(1- \theta)\frac{Y_t}{H_t} \end{eqnarray*} と表現できる。ただし、 \begin{eqnarray*} C_t &=& Y_t + (1- \delta)K_t - K_{t+1},\\ Y_t &=& \lambda_t K_t^{\theta} H_t^{1- \theta}, \\ r_t &=& \theta \frac{Y_t}{K_t} \end{eqnarray*} である。以上がHansenモデルの動学システムを記述している。\(\lambda_t = \bar{\lambda}e^{z_t}\)とする。

　確率的外的撹乱過程は \[ z _{t+1} =\gamma z_t + \epsilon _{t+1} \] で表現される。ここで、\(\epsilon _t\)は外生的確率過程である。

# This program shows the simulation results for the log-linearlized version of the basic RBC model
theta=.36; delta=.025; beta=.99; gamma=0.95

from numpy import *
import matplotlib.pyplot as plt

def varratio(ax,bw,cx,dw,roe,tol):
  '''
 compute the ratio of the variance of a jump variables to the variance of  the shock.
 The interation limit is 1000.
 The dynamical system:x_(t+1)=a x_t + b w_t, y_t = c x_t + d w_t,
 shock is w_(t+1)=roe w_t + epsilon_t
 function name: varratio(a,b,c,d,roe,tol)
  '''
  vr=0
  for i in range(1000):
    shortsum=0
    if i == 1:
      shortsum=1
    else:
      for j in range(i+1):
        shortsum=shortsum+ax**(j-1)*roe**(i+1-j)
    increment=cx*bw*shortsum+dw*roe**i
    vr=vr+increment*increment
    if abs(increment)<tol:
      #print 'the iterations are ended when i=',i,'since increments < ',increment
      break
  vr=vr+dw*dw
  return vr

# compute the value of Hbar when A=1.72
a0=1.72
Hbar=(1-(beta*delta*theta)/(1-beta*(1-delta)))
Hbar=1/(1+a0*Hbar/(1-theta))
print ("Hbar =", Hbar)

# compute the value of kbar
f0=theta/(1/beta-(1-delta))
Kbar=Hbar*f0**(1/(1-theta))
print ("Kbar =", Kbar)

# set up the matrices necessary for the eqiulibrium law of motion
rbar=1/beta-(1-delta)
ybar=(Kbar**theta) * (Hbar**(1-theta))
cbar=ybar-delta*Kbar
A=array([[0.], [-Kbar], [0.],[0.]])
B=array([[0.], [(1-delta)*Kbar], [theta], [-1.]])
C=array([[1.,  -1.,  -1./(1-Hbar), 0.0],
            [ybar, -cbar, 0., 0.],
            [-1., 0., 1-theta, 0],
            [1., 0., 0., -1.]])
D=array([[0.], [0.], [1.], [0.]])
F=0.
G=F
H=F
J=array([0., -1., 0., beta*rbar])
K=array([0., 1., 0., 0.])
L=F
M=F
N=.95
print ("A=",A)
print ("B=",B)
print ("C=",C)
print ("D=",D)

# solve the Ricatti equation for P

Cinv=linalg.inv(C)
CinvA=dot(Cinv,A)
a = F-dot(J,CinvA)
CinvB=dot(Cinv,B)
b = -(dot(J,CinvB)-G + dot(K,CinvA))
c = -dot(K,CinvB)+H
P1 = (-b+sqrt(b**2-4*a*c))/(2*a)
P2 = (-b-sqrt(b**2-4*a*c))/(2*a)
if abs(P1)<1:
    P=P1
else:
    P=P2

print ("P=",P)
      
# the eqiulibrium law of motion is x(t)=Px(t-1)+Qw(t), y(t)=Rx(t-1)+Sw(t)
# x= capital(state variable)
# y=[output, consumption, labor, interest_rate](jump variables:non-predetermined)
# w is AR(1) process.

AP=A*P
CinvD=dot(Cinv,D)
R=-dot(Cinv,AP+B)
print ("R=",R)

JCinvA=dot(J,CinvA)
JCinvD=dot(J,CinvD)

Q=(JCinvD-L)*N + dot(K,CinvD)-M

QD=N*(F-JCinvA)+ F*P + G + dot(J,R)- dot(K,CinvA)
Q=Q/QD
print ("Q=", Q)
AQ=A*Q
S=-dot(Cinv, (AQ+D))
print ("S=", S)

# compute the impulse response function for the technology shock =1
# the eqiulibrium law of motion is x(t)=Px(t-1)+Qw(t), y(t)=Rx(t-1)+Sw(t), w(t) = N w(t-1) + shock(t)

runlgth=100
x=zeros(100)
y=zeros((4,100))
w=zeros(100)
wold=0.
shock=zeros(100)
shock[0]=1.
xold=0.

for i in range(100):
       w[i]=N*wold+shock[i]       
       x[i]=P*xold+Q*wold
       for j in range(4):
           y[j,i]=R[j]*xold + S[j]*wold

xold=x[i]
       wold=w[i]
    
time=arange(0.,100,1.)
plt.subplot(2,1,1)
plt.plot(time, x,'k', label='capital')
plt.xlabel('time')
plt.ylabel('state variable')
plt.title('the impulse response of state and jump variables to technology shock',fontsize=16)
plt.legend()
plt.subplot(2,1,2)
plt.plot(time,y[0,:],'b',label='output')
plt.plot(time,y[1,:],'r',label='consumption')
plt.plot(time,y[2,:],'g+',label='labor')
plt.plot(time,y[3,:],'k',label='interest rate')
plt.xlabel('time')
plt.ylabel('jump variables')
plt.legend()

# compute the ratio of the variance of variable to the shock variance

print ('The standard error ratios of the jump variables to the technology shock \n are as follows:')

vr=varratio(P,Q,R[0],S[0],gamma,0.1e-10)
std=sqrt(vr)
print ('Y_sigma=', std)
vr=varratio(P,Q,R[1],S[1],gamma,0.1e-10)
std=sqrt(vr)
print ('C_sigma=',std)
vr=varratio(P,Q,R[2],S[2],gamma,0.1e-10)
std=sqrt(vr)
print ('H_sigma=', std)
vr=varratio(P,Q,R[3],S[3],gamma,0.1e-10)
std=sqrt(vr)
print ('r_sigma=', std)

plt.show()

　以上を記述したプログラムを実行すると、以下の結果が得られる。Uhlig が提案した方法に従って、モデルの対数線形化を行っています。外生的撹乱はステップ状撹乱としている。

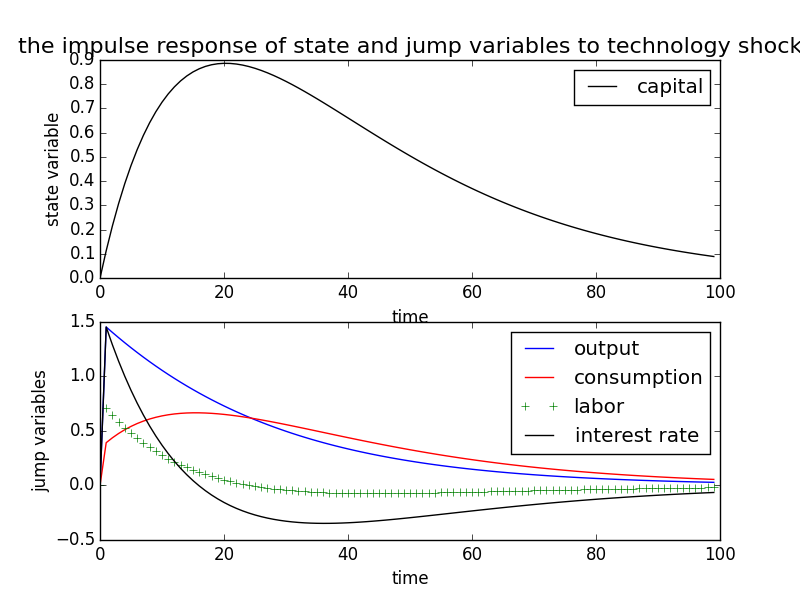
Hansen_model_demo

networkX の初歩

　以下では、Pythonのsite-package networkxがインストールされていることを前提とします。例えば、Anacondaを用いてPythonをインストールすると、networkxも一括してインストールされるので、即座に利用可能となります。グラフを表示するためには、matplotlibパッケージが必要なので、この使用方法についても知識があると想定します。また、Colabolatory を活用して、Netwrkx を簡単に利用することもできます。

　networkx はバージョンが neworkx 2.0 のアップデートされています。コードの仕様がかなり変更されていますので、 networkx 1.0 を前提に書かれたコードは重大なエラーを出します。以下のコードは networkx 1.0 で書かれたものです。 neworkx 2.0 で書かれたコードの紹介は、このページにあります。

ネットワークを作成するためには、作成するネットワークに名前を付ける必要がある。
import networkx as nx
G=nx.Graph()
と記述すると、名前がGという（空の）ネットワークが作成される。このGに必要なノードとリンクを付け加えて、作成すべきネットワークを構成して行く。以下の例は10個のノードからなるネットワークを描くscriptである。Nはノードの集合、Eはリンクの集合を定義している。
G.add_nodes_from(N)
で、Nで与えられたノードを加え、
G.add_edges_from(E)
と書くと、集合Eのリンクをもつネットワークが出来上がる。# drawing ...以下の記述はこのネットワークをグラフィックに描くコードになっている。

# -*- coding: utf-8 -*- 
# creating a new network 
import networkx as nx 

G = nx.Graph() 
N=[1,2,3,4,5,6,7,8,9,10]
E= [(1,2),(1,8),(2,3),(2,4),(4,5),(6,7),(6,8),(8,9),(8,10)]
G.add_nodes_from(N)
G.add_edges_from(E)
# drawing the created network 
import matplotlib.pyplot as plt
 
nx.draw_networkx(G,with_labels=True, node_color='r') 
plt.axis('off')
plt.title('an example')
plt.savefig("example.png") # save as png
plt.show()

このscriptを実行すると、以下のようなネットワークの図が表示される。plt.savefig('example.png')は'example'という名前の画像ファイルをpng形式で保存させるための命令文である。

このページのトップに戻る

ホームページに戻る